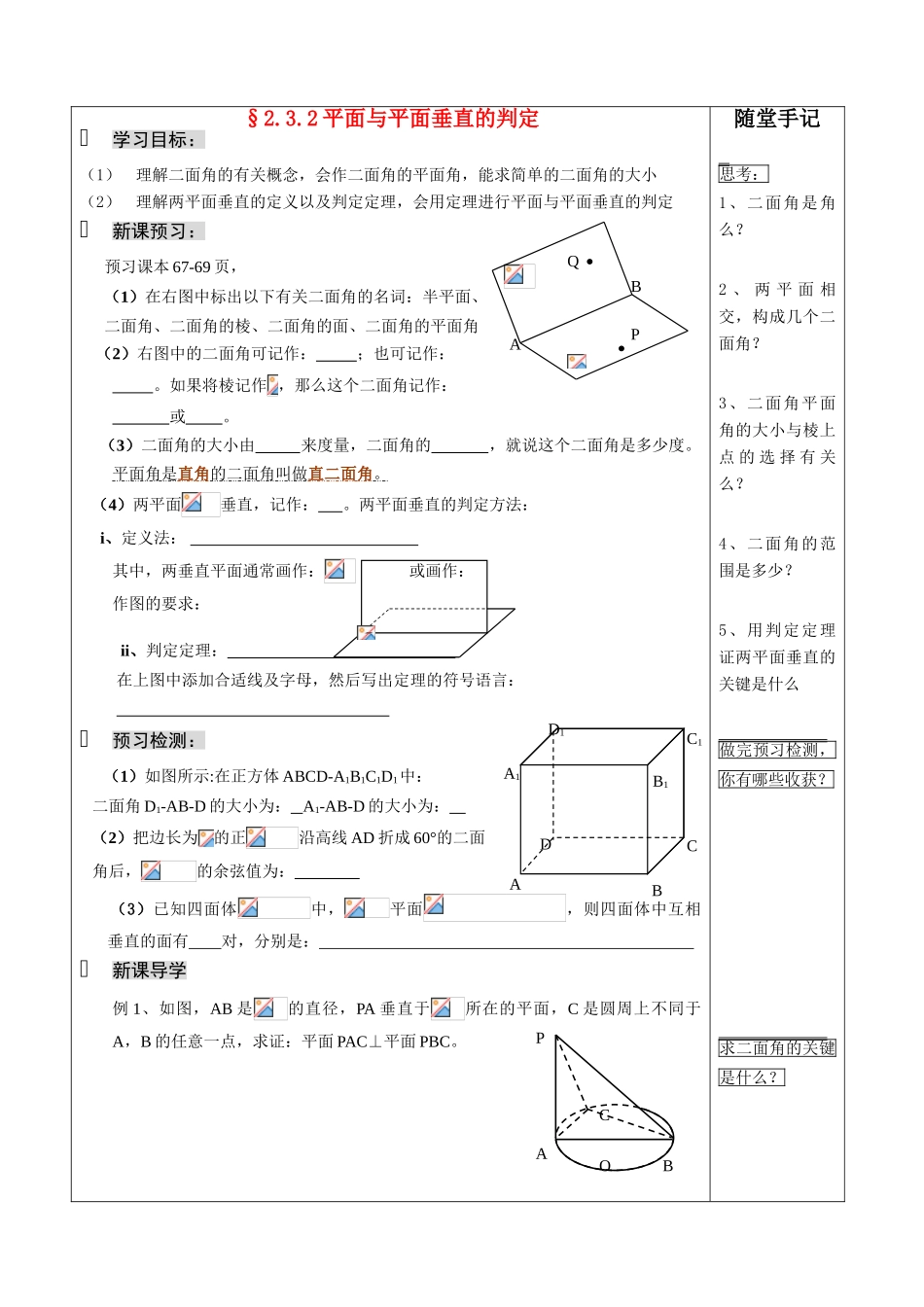
§2.3.2 平面与平面垂直的判定学习目标:(1)理解二面角的有关概念,会作二面角的平面角,能求简单的二面角的大小(2)理解两平面垂直的定义以及判定定理,会用定理进行平面与平面垂直的判定新课预习:预习课本 67-69 页,(1)在右图中标出以下有关二面角的名词:半平面、二面角、二面角的棱、二面角的面、二面角的平面角(2)右图中的二面角可记作: ;也可记作: 。如果将棱记作 ,那么这个二面角记作: 或 。 (3)二面角的大小由 来度量,二面角的 ,就说这个二面角是多少度。平面角是 直角 的二面角叫做 直二面角 。 (4)两平面垂直,记作: 。两平面垂直的判定方法: i、定义法: 其中,两垂直平面通常画作: 或画作: 作图的要求: ii、判定定理: 在上图中添加合适线及字母,然后写出定理的符号语言: 预习检测:(1)如图所示:在正方体 ABCD-A1B1C1D1中: 二面角 D1-AB-D 的大小为: A1-AB-D 的大小为: (2)把边长为的正沿高线 AD 折成 60°的二面 角后,的余弦值为: (3)已知四面体中,平面,则四面体中互相垂直的面有 对,分别是: 新课导学例 1、如图,AB 是的直径,PA 垂直于所在的平面,C 是圆周上不同于A,B 的任意一点,求证:平面 PAC⊥平面 PBC。随堂手记 思考:1、二面角是角么?2 、 两 平 面 相交,构成几个二面角?3、二面角平面角的大小与棱上点 的 选 择 有 关么?4、二面角的范围是多少?5、用判定定理证两平面垂直的关键是什么 做完预习检测,你有哪些收获? 求二面角的关键是什么?COPBAPABQAA1BCDB1D1C1练习 1、如图,在三棱锥中,,试判断平面与平面之间的位置关系,并说明理由。 例 2、如图,是二面角的棱上的一点,分别在上引射线,如果。求二面角的大小。 练习 2、在二面角中,于。 ,求二面角的大小。 知识巩固:1、若一个二面角的两个面所在的平面分别平行于另一个二面角的两个面所在的平面,则这两个二面角的关系为 ( )A、相等 B、互补 C、相等或互补 D、无法确定2、在正方体中,二面角的大小为 3、在四面体中,。求证:平面平面。4、如图,已知在中, 课后反思:本节课你的收获有哪些?还有没有需要老师帮助解决的问题? 随堂手记BAPMNVABC。求证:平面平面。ECDBA