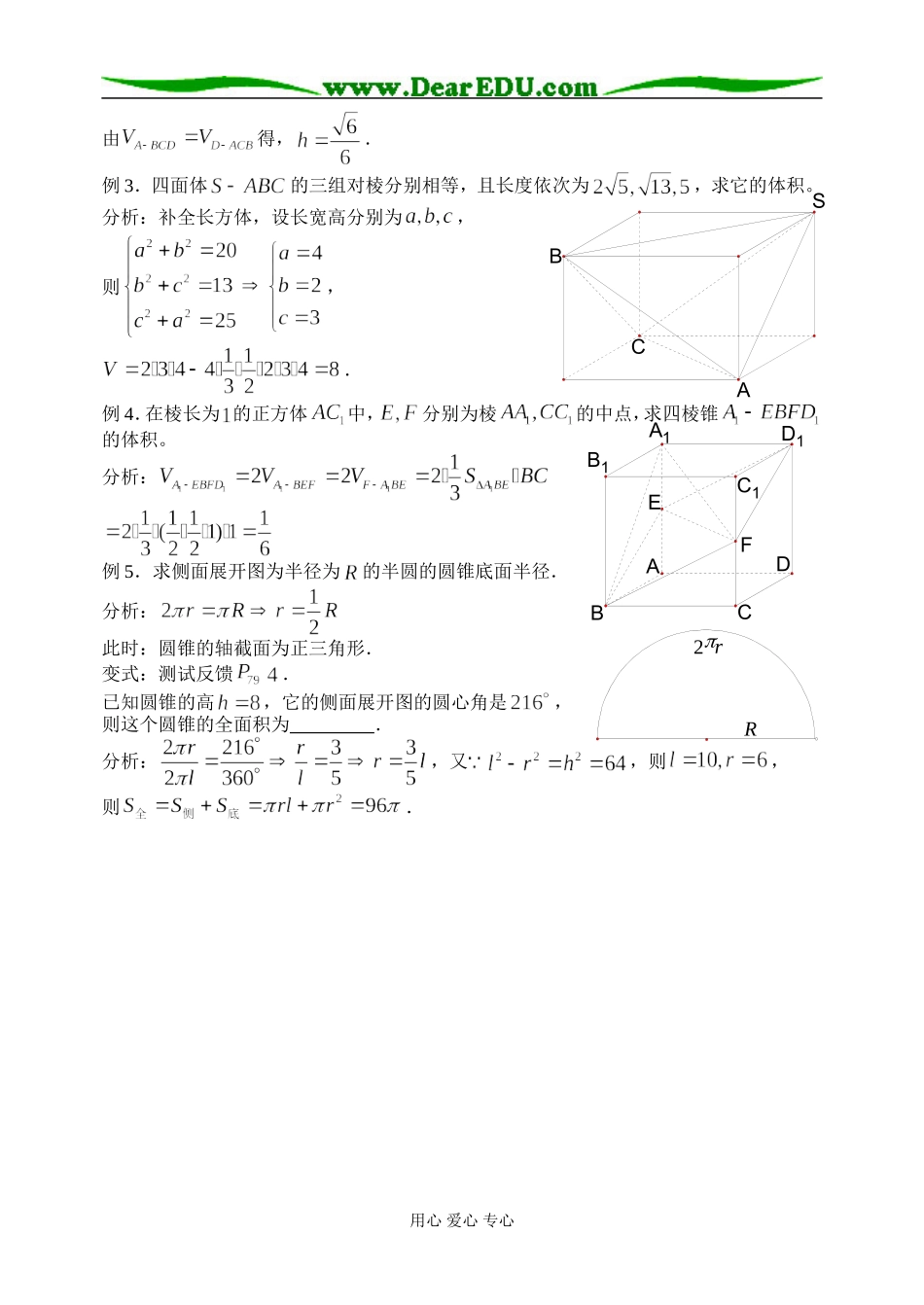
ODACBSSACDB§1.3.2 柱、锥、台体的表面积与体积教学目标:1.掌握直(正)棱柱、正棱锥、正棱台的侧面积公式2.掌握柱、锥、台体的体积公式3.掌握求体积的方法:补形,转换,等积,会用等积法求点到面的距离教学重点:求体积的方法:补形,转换,等积教学难点:求体积的方法:补形,转换,等积教学过程:例 1.一个正三棱锥的高和底面边长都是 ,求它的侧面积、表面积、体积。分析:在中,,则斜高,,,.注:(1)解棱锥问题时,注意抓住两个直角三角形,即和,利用这两个三角形可以在高、斜高、侧棱之间相互求解。(2)即侧棱与底面所成角,即侧面与底面所成二面角的平面角,侧面与底面所成角就是斜高与底面所成角.例 2.一个正三棱锥的侧棱和底面边长都是 ,求它的体积。分析:方法一:同例 1,可得.方法二:(补形)补全正方体,则,,(等积转换)注:求三棱锥体积时,注意运用三棱锥的特殊性,即三棱锥的每个面都是三角形,则每个面都可以作为底面,每个点都可以最为顶点.应用:求点到平面的距离.(等积法求点到面的距离),,用心 爱心 专心SCABFED1A1C1B1DABCR2r由得,.例 3.四面体的三组对棱分别相等,且长度依次为,求它的体积。分析:补全长方体,设长宽高分别为,则,.例 4.在棱长为 的正方体中,分别为棱的中点,求四棱锥的体积。分析:例 5.求侧面展开图为半径为的半圆的圆锥底面半径.分析:此时:圆锥的轴截面为正三角形.变式:测试反馈.已知圆锥的高,它的侧面展开图的圆心角是,则这个圆锥的全面积为 .分析:,又,则,则.用心 爱心 专心