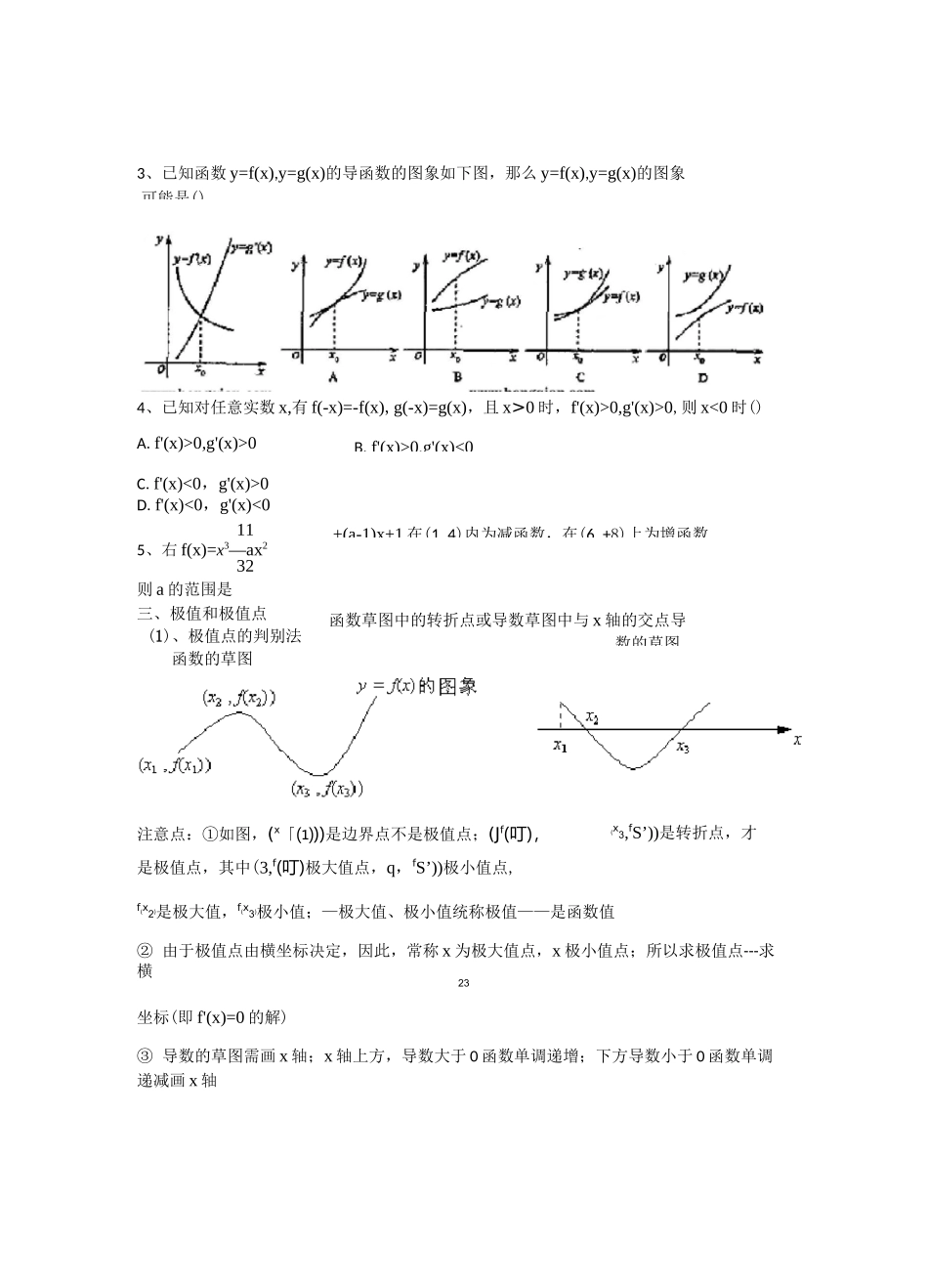
导数一、导数公式(1) 、几种常见的导数①C'=;②(xa)'=(awR);③(ax)'二=;®(ex)'二;⑤ (logx)'二=;a⑥ (lnx)'二;⑦(sinx)'二;⑧;(cosx)'二(2) 、导数运算规则:①[k-f(x)]'二;②[f(x)土 g(x)]'二;③[f(x)-g(x)]y;④=;sinx练习:1、函数 y=——的导数为;x2、若 f(x)二 x2lnx,则 f'(x)二3、若 f(x)=sina-cosx,则 f'(a)=二、函数的单调性f(x)丰 C,f(x)在区间 A 单调递增 Of'(x)>0 在 A 恒成立f(x)丰 C,f(x)在区间 A 单调递减 Of'(x)<0 在 A 恒成立作用:可求单调区间 O 解不等式;或判定函数在某区间单调;常识:看到单调,就想到导数大于等于(或小于等于)0 在给定区间恒成立练习:1、已知 f(x)二 ax3+3x2-x+1 在 R 上是减函数,则 a 的取值范围是 2、设 f'(x)是函数 f(x)的导函数,y=f'(x)的图象如图(1)所示,则 y=f(x)的图象最B.f'(x)>0,g'(x)<0+(a-1)x+1 在(1,4)内为减函数,在(6,+8)上为增函数,函数草图中的转折点或导数草图中与 x 轴的交点导数的草图3、已知函数 y=f(x),y=g(x)的导函数的图象如下图,那么 y=f(x),y=g(x)的图象4、已知对任意实数 x,有 f(-x)=-f(x),g(-x)=g(x),且 x>0 时,f'(x)>0,g'(x)>0,则 x<0 时()A.f'(x)>0,g'(x)>0C.f'(x)<0,g'(x)>0D.f'(x)<0,g'(x)<0115、右 f(x)=x3—ax232则 a 的范围是三、极值和极值点(1)、极值点的判别法函数的草图是极值点,其中(3,f(叮)极大值点,q,fS’))极小值点,f(x2)是极大值,f(x3)极小值;—极大值、极小值统称极值——是函数值② 由于极值点由横坐标决定,因此,常称 x 为极大值点,x 极小值点;所以求极值点---求横23坐标(即 f'(x)=0 的解)③ 导数的草图需画 x 轴;x 轴上方,导数大于 0 函数单调递增;下方导数小于 0 函数单调递减画 x 轴可能是()注意点:①如图,(x「⑴))是边界点不是极值点;(Jf(叮),(x3,fS’))是转折点,才x(2)、求函数 y=f(x)的极值的方法:① 求出 f'(x)=0 的根 X;②利用导数草图判定 X 是极大值点还是极小值点;③求出极ii值(3) 求最值的方法① 求出 f'(x)=0 的根 X;②作出导数草图;③作出函数草图;④计算比较得到最值i练习:1、①已知函数 f(X)二 X3-12X+8 在区间[—3,3]上的最大值为 M,则 M 二.②f(X)=—X4+2X2+3 在(一 a,2)的值域是2、已知 f(X)二 X3+bx2+cx。如图,y=f'(x)的图象过点(1,0),(2,0),则下列说法中:不正确的有3① X=时,函数...