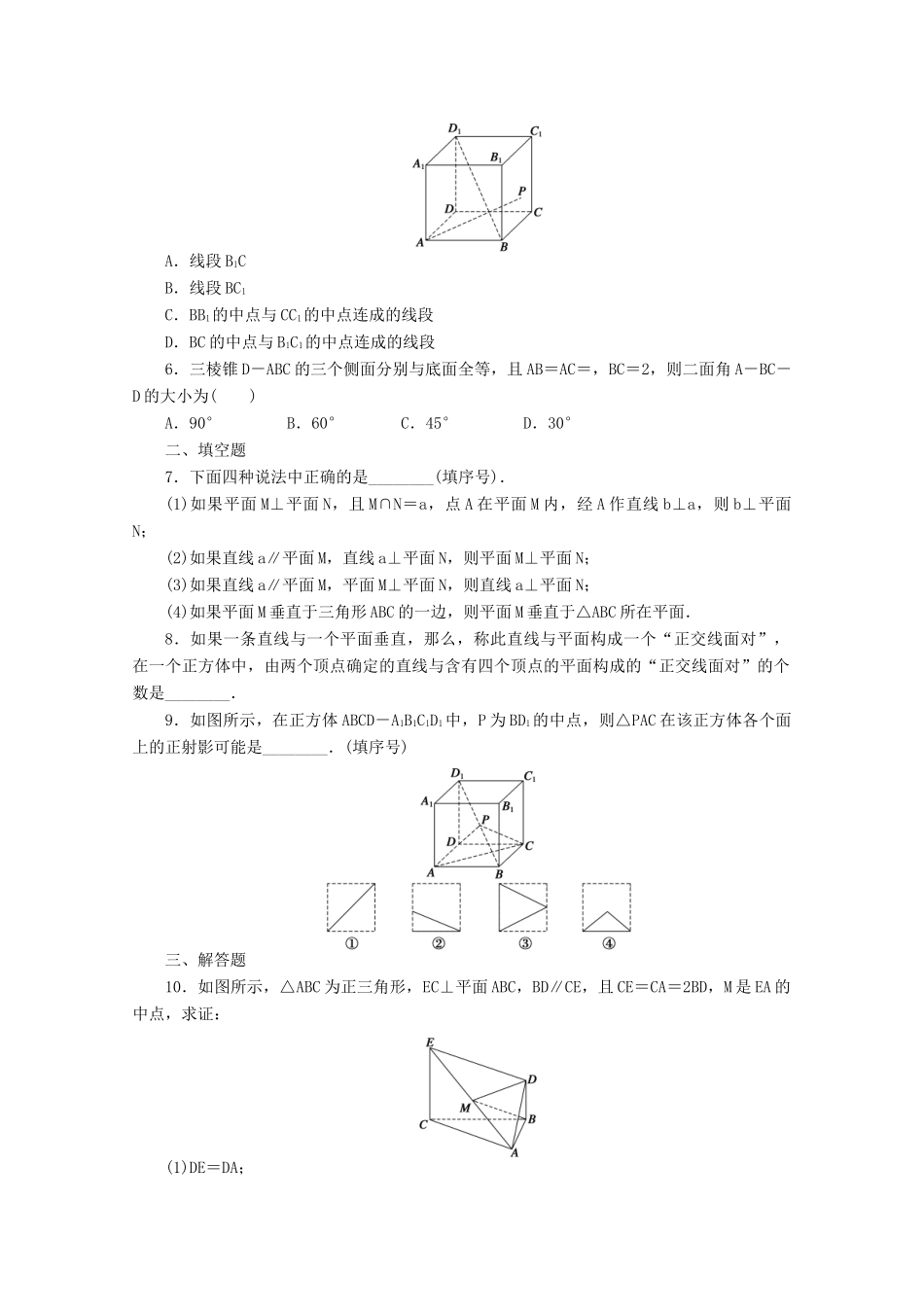
习题课(一)【课时目标】 1.能熟练应用直线、平面平行与垂直的判定及性质进行有关的证明.2.进一步体会化归思想在证明中的应用.a、b、c 表示直线,α、β、γ 表示平面.位置关系判定定理(符号语言)性质定理(符号语言)直线与平面平行a∥b 且__________⇒a∥αa∥α,____________⇒a∥b平面与平面平行a∥α,b∥α,且________________⇒α∥βα∥β,________________⇒a∥b直线与平面垂直l⊥a,l⊥b,________________⇒l⊥αa⊥α,b⊥α⇒______平面与平面垂直a⊥α,________⇒α⊥βα⊥β,α∩β=a,__________⇒b⊥β一、选择题1.不同直线 m、n 和不同平面 α、β.给出下列推论:①⇒m∥β; ②⇒n∥β;③⇒m,n 异面; ④⇒m⊥β.其中错误的有( )A.0 个 B.1 个 C.2 个 D.3 个2.下列说法中:(1)平行于同一直线的两个平面平行;(2)平行于同一平面的两个平面平行;(3)垂直于同一直线的两直线平行;(4)垂直于同一平面的两直线平行.其中正确的个数有( )A.4 个 B.1 个 C.2 个 D.3 个3.若 a、b 表示直线,α 表示平面,下列推论中正确的个数为( )①a⊥α,b∥α⇒a⊥b;② a⊥α,a⊥b⇒b∥α;③a∥α,a⊥b⇒b⊥α.A.1 B.2 C.3 D.04.过平面外一点 P:①存在无数条直线与平面 α 平行;②存在无数条直线与平面 α 垂直;③有且只有一条直线与平面 α 平行;④有且只有一条直线与平面 α 垂直,其中正确的个数是( )A.1 B.2 C.3 D.45.如图所示,正方体 ABCD-A1B1C1D1中,点 P 在侧面 BCC1B1及其边界上运动,并且总是保持 AP⊥BD1,则动点 P 的轨迹是( )A.线段 B1CB.线段 BC1C.BB1的中点与 CC1的中点连成的线段D.BC 的中点与 B1C1的中点连成的线段6.三棱锥 D-ABC 的三个侧面分别与底面全等,且 AB=AC=,BC=2,则二面角 A-BC-D 的大小为( )A.90° B.60° C.45° D.30°二、填空题7.下面四种说法中正确的是________(填序号).(1)如果平面 M⊥平面 N,且 M∩N=a,点 A 在平面 M 内,经 A 作直线 b⊥a,则 b⊥平面N;(2)如果直线 a∥平面 M,直线 a⊥平面 N,则平面 M⊥平面 N;(3)如果直线 a∥平面 M,平面 M⊥平面 N,则直线 a⊥平面 N;(4)如果平面 M 垂直于三角形 ABC 的一边,则平面 M 垂直于△ABC 所在平面.8.如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”...