3.2.3 指数函数与对数函数的关系一、教学目标:1、了解反函数的概念。 2、理解互为反函数图象间的关系。 3、掌握对数函数与指数函数互为反函数。 重点:反函数的概念及互为反函数图象间的关系。 难点:反函数的概念。二、知识梳理1 、 当 一 个 函 数 是 一 一 映 射 时 , 可 以 把 这 个 函 数 的 因 变 量 作 为 一 个 新 的 函 数 的 而 把 这 个 函 数 的 自 变 量 作 为 新 的 函 数 的 我 们 称 这 两 个 函 数 为 即的反函数记作 。2、互为反函数的图象关于直线 对称;互为反函数的图象同增同减。3、指数函数与对数函数有何内在关系①反解出= ② 和互换位置 。4、什么样的函数没有反函数?5、当 a>1 时,在区间内,指数函数 y=随着 x 的增加,函数值的增长速度 ,而对数函数 y=增长的速度 。三、例题解析例 1、求,()的反函数.例 2、求的反函数.例 3、求的反函数.结论:根据以上几个题目,求反函数的一般步骤:①、由,解出;②、交换得;③、根据的值域,写出的定义域.变式训练:课本 106 页练习 A、练习 B。限时训练:1、已知函数 y=ex的图像与函数 y=f(x)的图像关于直线 y=x 对称,则 A、f(2x)=e2x x R B、f(2x)=ln2 lnx (x>0) C、f(2x)=2ex x R D、f(2x)=ln2 +lnx (x>0)2、已知函数 y=与其反函数的图像有交点,设交点的横坐标为 x0,则 A、a>1 且 x0>1 B、0
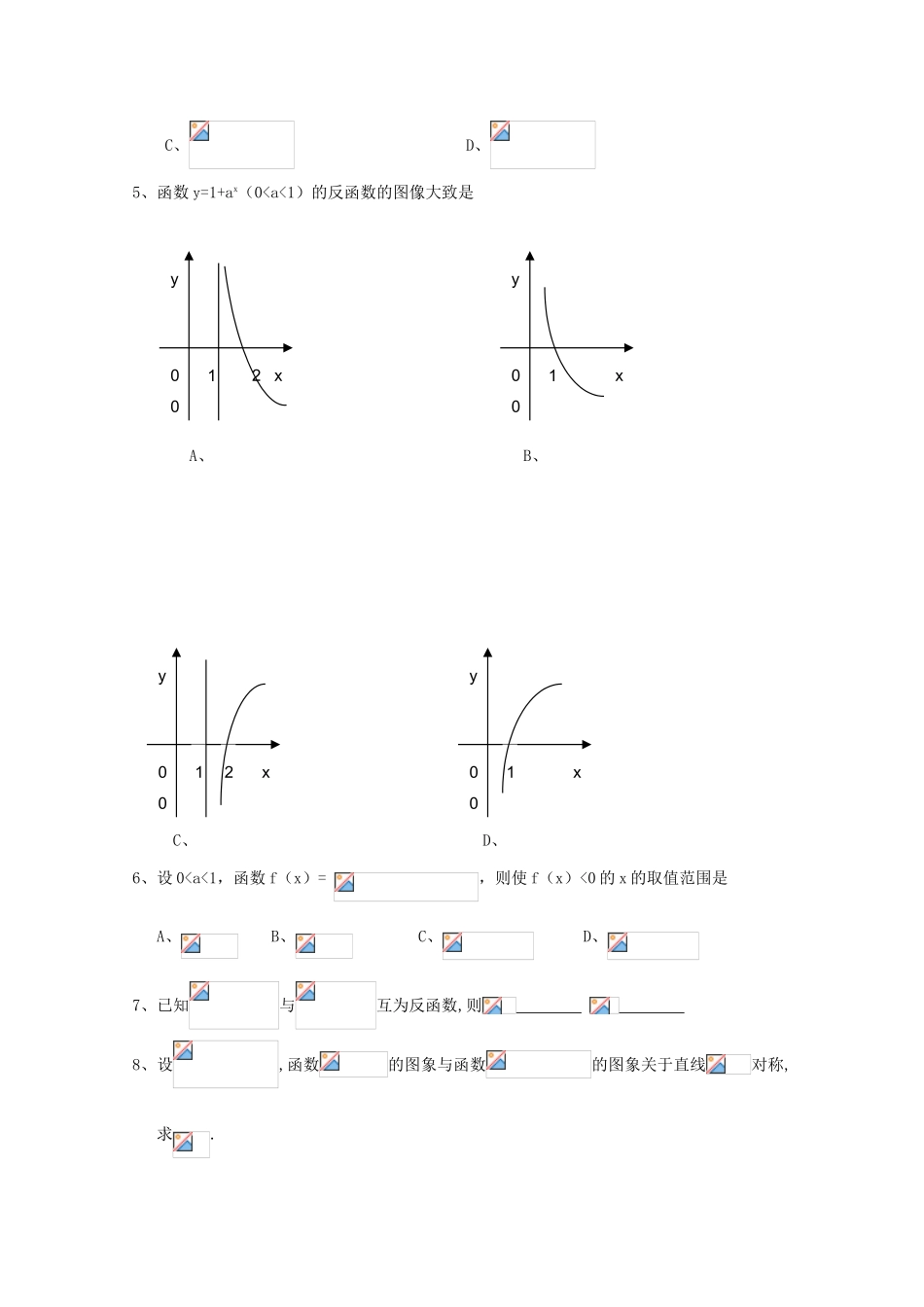
1 且 0< x0<1 D、013、设 a>0,a 1,函数 f(x)= ,g(x)= 的反函数分别是和。若lga+lgb=0,则和的图像 A、关于 x 轴对称 B、关于 y 轴对称 C、关于原点对称 D、关于 y=x 对称 4、函数 y=21-x+3(x R)的反函数的解析表达式为 A、 B、 C、 D、5、函数 y=1+ax(0