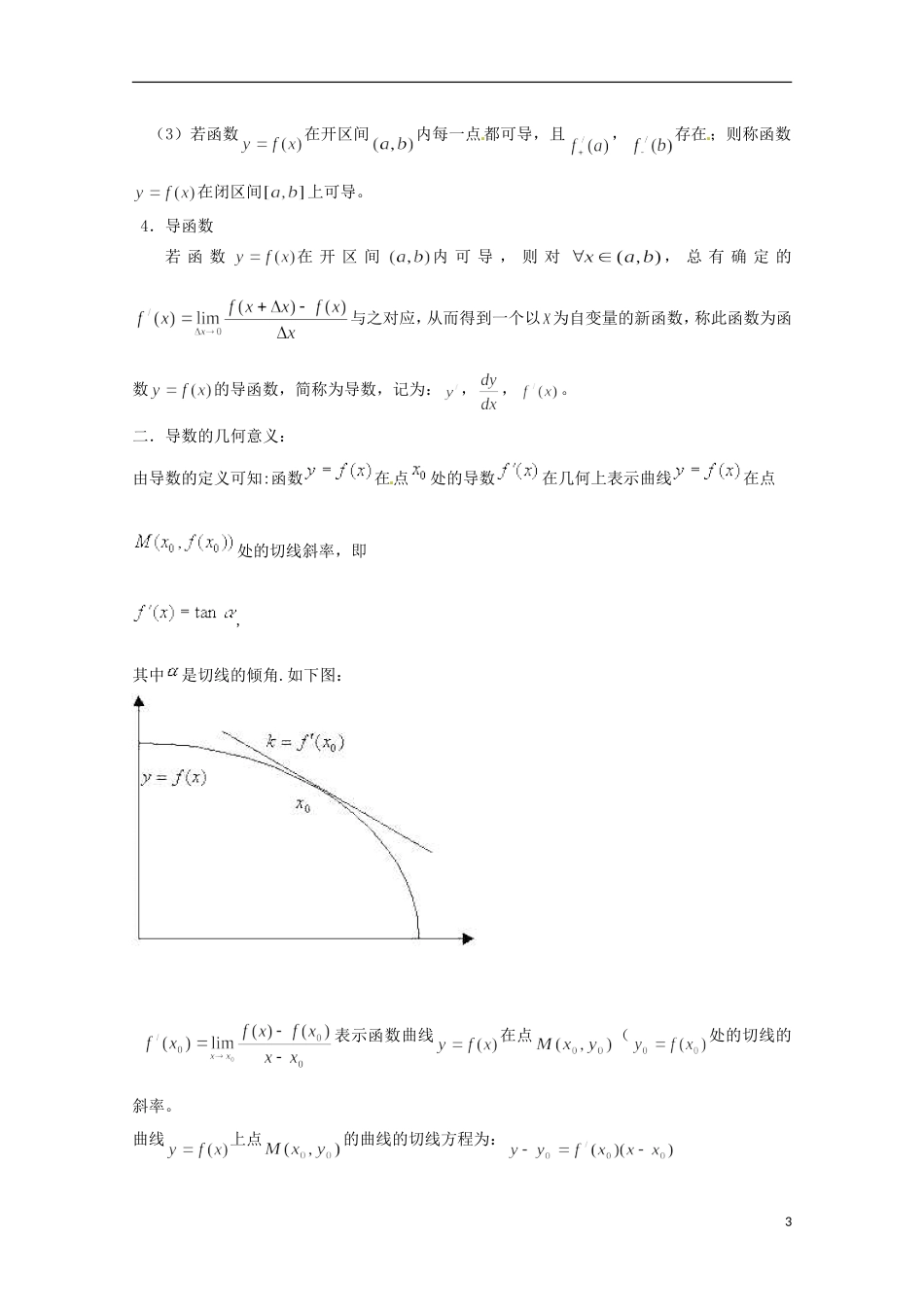
2013 年高中数学 1.1 2 导数概念教案 新人教 A 版选修 2-2一.导数的定义1.引例例 1:变速直线运动的速度 设有一物体 M,沿直线从 O 点开始作变速直线运动,在 时刻运动到点 P,与点 O 的距离为,求物体 M 在时刻的瞬时速度。 已知匀速直线运动的速度为:, 变速直线运动在到这一时间段内的平均速度为,如果当时,上式的极限存在,记为,即。即为所求的物体 M 在时刻的瞬时速度。例 2:曲线的切线问题2.导数的定义 定义 1:设函数在点的某一邻域内有定义,当自变量 在处取得增量(+仍在该邻域内)时,相应地函数取得增量;如果与之比当时的极限存在,则称函数在点处可导,并称此极限值为函数在点处的导数(微商),记作:,,。即:注:(1)函数在点处可导,亦可称函数在点处的导数存在(或具有导数)1 (2)函数导数的另外两种定义:,。 (3)如果不存在,称函数在点处不可导。 (4)/为函数在区间(或)上的平均变化率;而导数是因变量在点对于 的变化率,反映因变量随自变量 的变化而变化的快慢程度。导数的概念就是函数变化率这一概念的精确描述。(5)根据导数的定义和极限存在的充要条件,相应地定义函数在点处右可导、左导数如下(分别记右可导、左导数为,): , 。且有:函数在点处可导函数在处,、都存在,= . (即函数在点处可导数的充要条件是函数在点处既右可导、有左可导)。 3.函数在区间上(内)可导的概念: (1)若函数在开区间内每一点都可导,则称函数在开区间内可导。 (2)若函数在开区间内每一点都可导,且存在,则称函数在区间上可导。2 (3)若函数在开区间内每一点 都可导,且,存在;则称函数在闭区间上可导。 4.导函数若 函 数在 开 区 间内 可 导 , 则 对, 总 有 确 定 的与之对应,从而得到一个以 为自变量的新函数,称此函数为函数的导函数,简称为导数,记为:,,。二.导数的几何意义:由导数的定义可知:函数在点处的导数在几何上表示曲线在点处的切线斜率,即,其中是切线的倾角.如下图: 表示函数曲线在点(处的切线的斜率。曲线上点的曲线的切线方程为:3曲线上点的曲线的法线方程为:。三.简单函数的导数例 2: 求函数(n 为正整数)在处的导数更一般地,对于幂函数(为常数),有例 3: 求函数的导数即 例 4:求函数的导数.解 :=即:这就是指数函数的导数公式,特殊地,当时,因,故有: 例 5:求函数的导数.4 例 6:求曲线在...