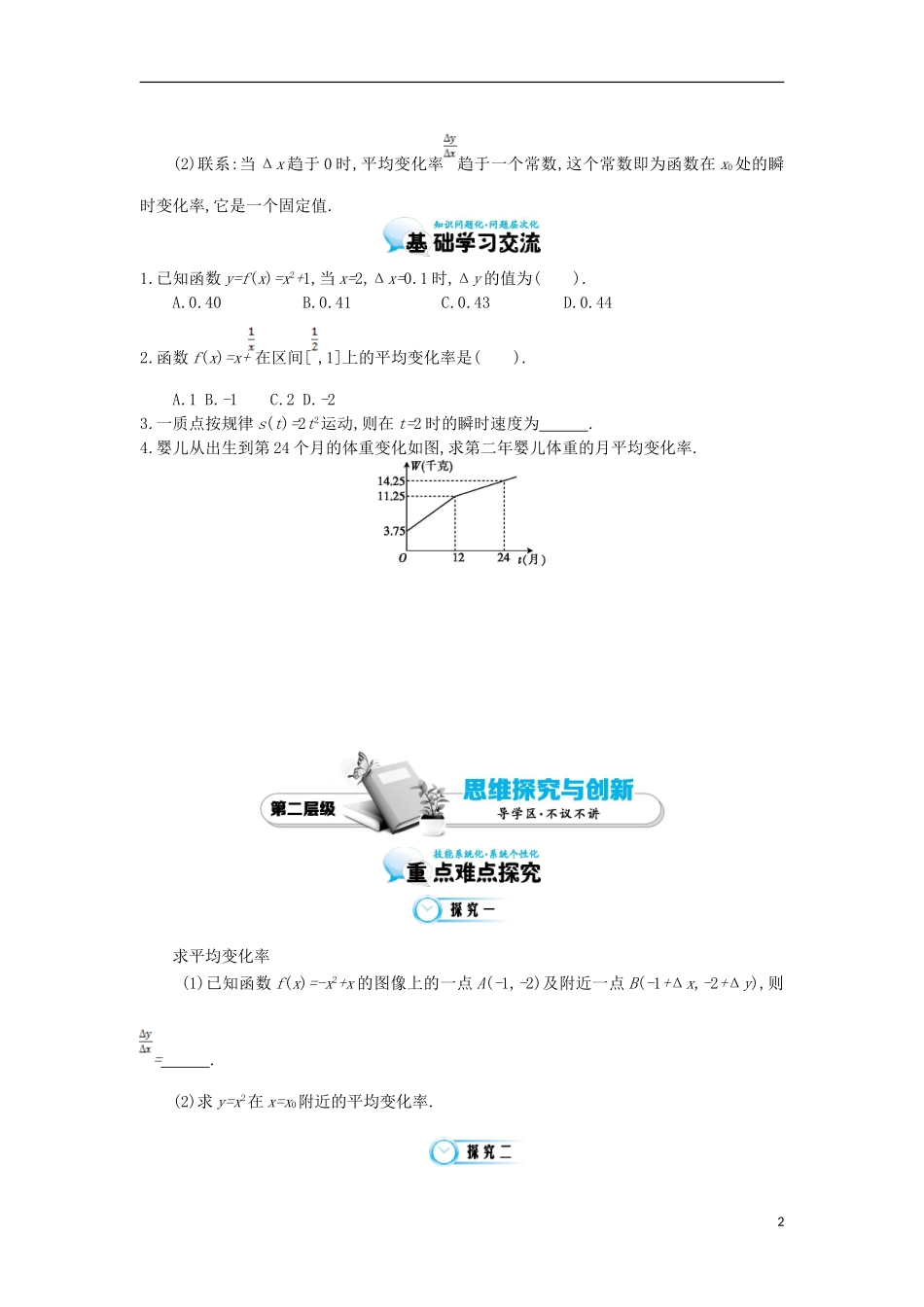
第 1 课时 变化的快慢与变化率1.通过物理中的运动了解平均变化率和瞬时变化率的概念.2.运用函数思想解决平均变化率问题.3.理解平均变化率的无限逼近思想得到瞬时变化率,初步体会极限的思想.借助多媒体播放 2012 年伦敦奥运会中国跳水运动员陈若琳夺得女子单人 10 米跳台冠军的视频.我们知道运动员的平均速度(平均变化率)不一定能够反映她在某一时刻的运动状态,而运动员在不同时刻的运动状态是不同的,我们需要借助于瞬时速度这样的量来刻画,那么我们如何才能求出运动员在某一时刻的瞬时速度呢?问题 1:根据以上情境,设陈若琳相对于水面的高度 h (单位:m)与起跳后的时间 t (单位:s) 存在函数关系 h(t)=-4.9t2+6.5t+10,如果用她在某段时间内的平均速度描述其运动状态, 那么:(1)在 0≤t≤0.5 这段时间里,运动员的平均速度 = . (2)在 1≤t≤2 这段时间里, 运动员的平均速度 = . 问题 2:函数 y=f(x)从 x1到 x2的平均变化率公式是 .如果用 x1与增量 Δx表示,平均变化率的公式是 . 问题 3:如何求函数的瞬时变化率?对一般的函数 y=f(x),在自变量 x 从 x0 变到 x1 的过程中,若设 Δx=x1-x0,Δy=f(x1)-f(x0),则函数的平均变化率是 == . 而当 Δx 趋于 0 时,平均变化率就趋于函数在 x0点的瞬时变化率,瞬时变化率刻画的是函数在一点处变化的快慢.问题 4:平均变化率与瞬时变化率的关系是什么?(1)区别:平均变化率刻画函数值在区间[x1,x2]上变化的快慢,瞬时变化率刻画函数值在点 x0处变化的快慢.1(2)联系:当 Δx 趋于 0 时,平均变化率趋于一个常数,这个常数即为函数在 x0处的瞬时变化率,它是一个固定值.1.已知函数 y=f(x)=x2+1,当 x=2,Δx=0.1 时,Δy 的值为( ).A.0.40 B.0.41 C.0.43 D.0.442.函数 f(x)=x+ 在区间[ ,1]上的平均变化率是( ).A.1 B.-1C.2 D.-23.一质点按规律 s(t)=2t2运动,则在 t=2 时的瞬时速度为 . 4.婴儿从出生到第 24 个月的体重变化如图,求第二年婴儿体重的月平均变化率.求平均变化率 (1)已知函数 f(x)=-x2+x 的图像上的一点 A(-1,-2)及附近一点 B(-1+Δx,-2+Δy),则= . (2)求 y=x2在 x=x0附近的平均变化率.2求物体运动的瞬时速度若一物体运动方程为 s=求此物体在 t=1 和 t=4 时的速度.求割线的斜率过曲线 y=f(x)=x3上两点 P(1,1)和 Q(1+Δx,1+Δy)作曲线的割线,求出当 Δx=0.1 时割线的斜率.函数 y=5x2+6 在区间[2,2+Δx]内的平均变化率...