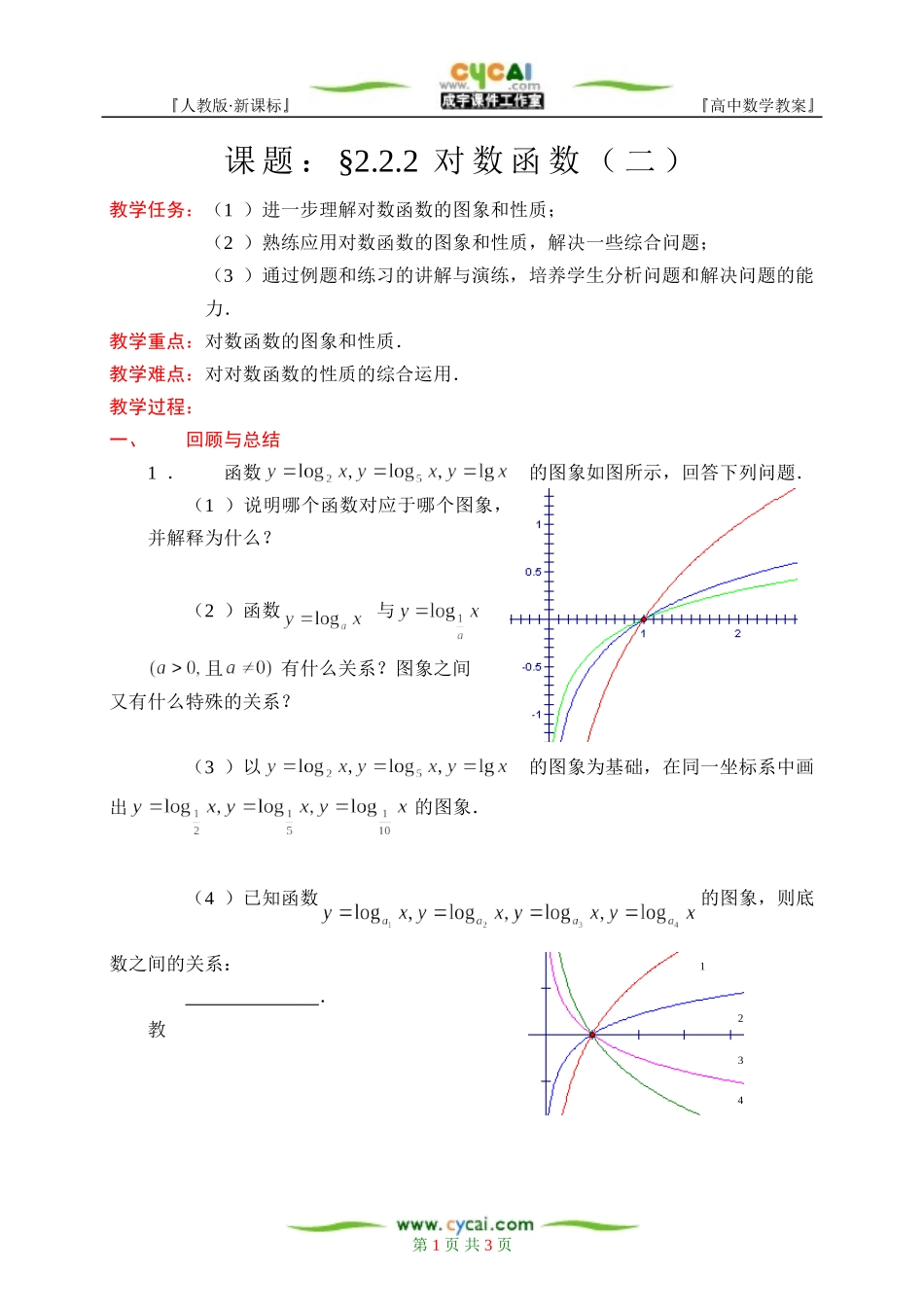
『人教版·新课标』 『高中数学教案』课 题 : §2.2.2 对 数 函 数 ( 二 ) 教学任务:(1 )进一步理解对数函数的图象和性质;(2 )熟练应用对数函数的图象和性质,解决一些综合问题;(3 )通过例题和练习的讲解与演练,培养学生分析问题和解决问题的能力.教学重点:对数函数的图象和性质.教学难点:对对数函数的性质的综合运用. 教学过程:一、回顾与总结1 .函数的图象如图所示,回答下列问题.(1 )说明哪个函数对应于哪个图象,并解释为什么?(2 )函数与且有什么关系?图象之间又有什么特殊的关系?(3 )以的图象为基础,在同一坐标系中画出的图象.(4 )已知函数的图象,则底数之间的关系: .教第 1 页 共 3 页 1 2 3 4『人教版·新课标』 『高中数学教案』2 .完成下表(对数函数且的图象和性质)图象定义域值域性质3 .根据对数函数的图象和性质填空. 已知函数,则当时, ;当时 , ; 当时 , ;当时, . 已知函数,则当时, ;当时 , ; 当时 , ; 当时 , ; 当时 , .二、应用举例例1 .比较大小: ,且; ,.解:(略)例2 .已知恒为正数,求的取值范围.解:(略)第 2 页 共 3 页『人教版·新课标』 『高中数学教案』[ 总结点评] :(由学生独立思考,师生共同归纳概括). .例3 .求函数的定义域及值域. 解:(略)注意:函数值域的求法.例4 .(1 )函数在[2 ,4] 上的最大值比最小值大1 ,求的值;(2 )求函数的最小值. 解:(略)注意:利用函数单调性求函数最值的方法,复合函数最值的求法.例5 .(2003年上海高考题)已知函数,求函数的定义域,并讨论它的奇偶性和单调性. 解:(略)注意:判断函数奇偶性和单调性的方法,规范判断函数奇偶性和单调性的步骤.例6 .求函数的单调区间.解:(略)注意:复合函数单调性的求法及规律:“同增异减”.练习:求函数的单调区间.三、作业布置考试卷一套第 3 页 共 3 页