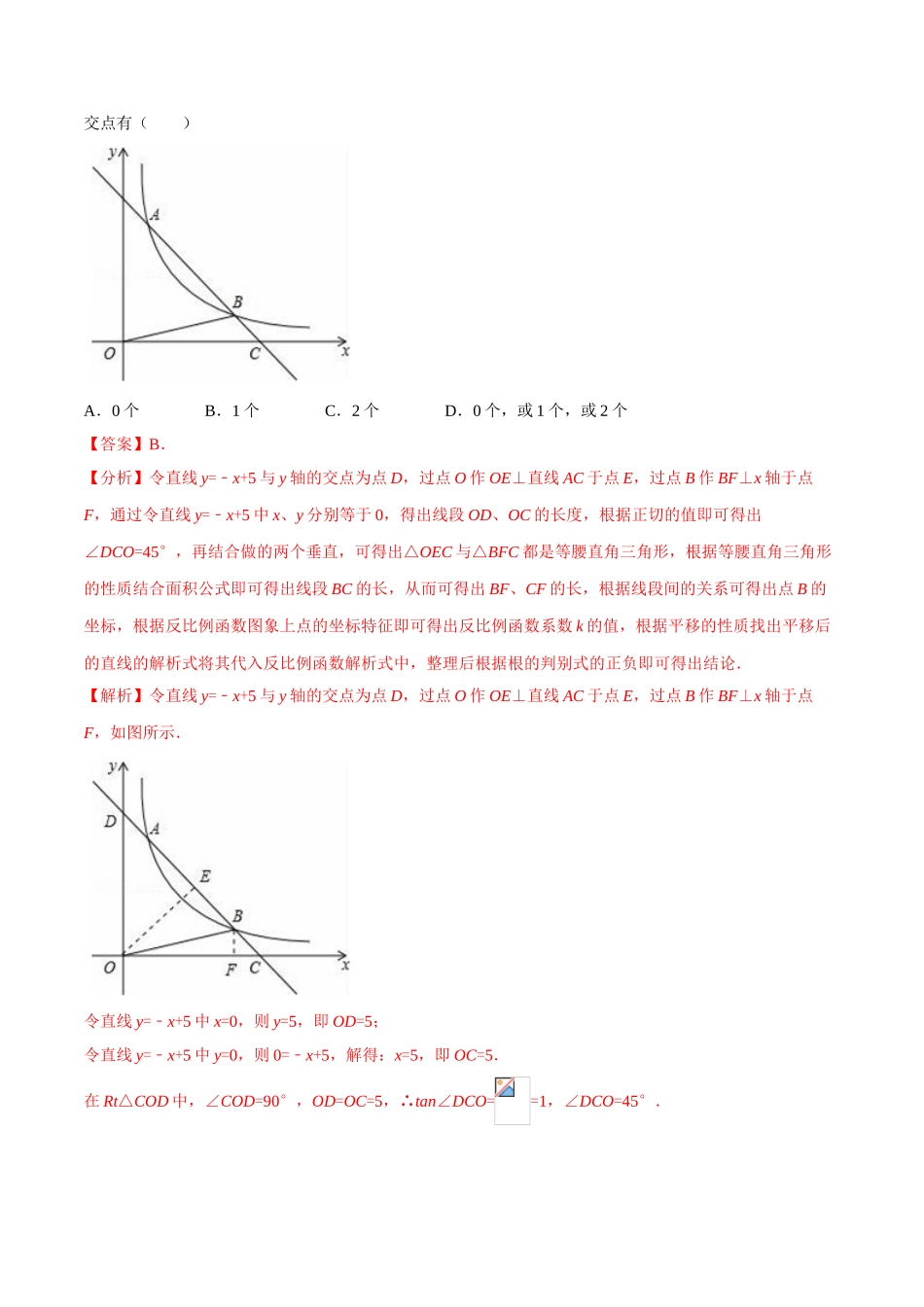
决胜 2024 中考数学压轴题全揭秘精品 专题 9 函数之一次函数和反比例函数综合问题专题 9:函数之一次函数和反比例函数综合问题一、选择题1.(2024 宁夏)正比例函数的图象与反比例函数的图象相交于 A,B 两点,其中点 B 的横坐标为﹣2,当时,x 的取值范围是( )A.x<﹣2 或 x>2 B.x<﹣2 或 0<x<2C.﹣2<x<0 或 0<x<2 D.﹣2<x<0 或 x>2【答案】B.【分析】由正、反比例函数的对称性结合点 B 的横坐标,即可得出点 A 的横坐标,再根据两函数图象的上下关系结合交点的横坐标,即可得出结论.【解析】 正比例和反比例均关于原点 O 对称,且点 B 的横坐标为﹣2,∴点 A 的横坐标为 2.观察函数图象,发现:当 x<﹣2 或 0<x<2 时,一次函数图象在反比例函数图象的下方,∴当时,x 的取值范围是 x<﹣2 或 0<x<2.故选 B.考点:反比例函数与一次函数的交点问题.2.(2024 山东省临沂市)如图,直线 y=﹣x+5 与双曲线(x>0)相交于 A,B 两点,与 x 轴相交于C 点,△BOC 的面积是.若将直线 y=﹣x+5 向下平移 1 个单位,则所得直线与双曲线(x>0)的交点有( )A.0 个 B.1 个 C.2 个 D.0 个,或 1 个,或 2 个【答案】B.【分析】令直线 y=﹣x+5 与 y 轴的交点为点 D,过点 O 作 OE⊥直线 AC 于点 E,过点 B 作 BF⊥x 轴于点F,通过令直线 y=﹣x+5 中 x、y 分别等于 0,得出线段 OD、OC 的长度,根据正切的值即可得出∠DCO=45°,再结合做的两个垂直,可得出△OEC 与△BFC 都是等腰直角三角形,根据等腰直角三角形的性质结合面积公式即可得出线段 BC 的长,从而可得出 BF、CF 的长,根据线段间的关系可得出点 B 的坐标,根据反比例函数图象上点的坐标特征即可得出反比例函数系数 k 的值,根据平移的性质找出平移后的直线的解析式将其代入反比例函数解析式中,整理后根据根的判别式的正负即可得出结论.【解析】令直线 y=﹣x+5 与 y 轴的交点为点 D,过点 O 作 OE⊥直线 AC 于点 E,过点 B 作 BF⊥x 轴于点F,如图所示.令直线 y=﹣x+5 中 x=0,则 y=5,即 OD=5;令直线 y=﹣x+5 中 y=0,则 0=﹣x+5,解得:x=5,即 OC=5.在 Rt△COD 中,∠COD=90°,OD=OC=5,∴tan∠DCO==1,∠DCO=45°. OE⊥AC,BF⊥x 轴,∠DCO=45°,∴△OEC 与△BFC 都是等腰直角三角形,又 OC=5,∴OE=. S...