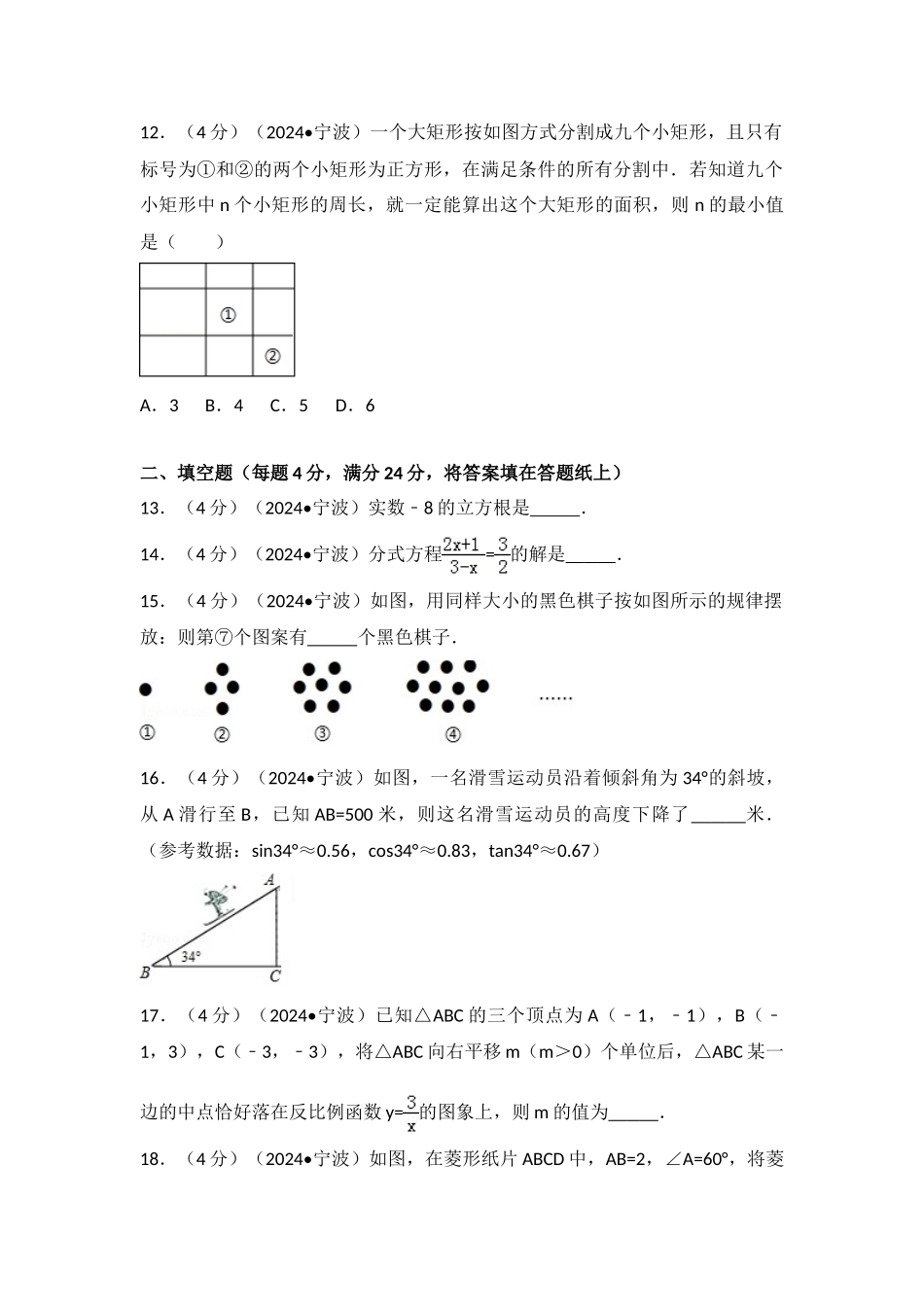
2024 年浙江省宁波市中考数学试卷 一、选择题:本大题共 12 个小题,每小题 4 分,共 48 分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(4 分)(2024•宁波)在,,0,﹣2 这四个数中,为无理数的是( )A.B.C.0D.﹣22.(4 分)(2024•宁波)下列计算正确的是( )A.a2+a3=a5 B.(2a)2=4a C.a2•a3=a5 D.(a2)3=a53.(4 分)(2024•宁波)2024 年 2 月 13 日,宁波舟山港 45 万吨原油码头首次挂靠全球最大油轮﹣﹣“泰欧”轮,其中 45 万吨用科学记数法表示为( )A.0.45×106吨 B.4.5×105吨 C.45×104吨D.4.5×104吨4.(4 分)(2024•宁波)要使二次根式有意义,则 x 的取值范围是( )A.x≠3B.x>3C.x≤3D.x≥35.(4 分)(2024•宁波)如图所示的几何体的俯视图为( )A.B.C.D.6.(4 分)(2024•宁波)一个不透明的布袋里装有 5 个红球,2 个白球,3 个黄球,它们除颜色外其余都相同,从袋中任意摸出 1 个球,是黄球的概率为( )A.B.C.D.7.(4 分)(2024•宁波)已知直线 m∥n,将一块含 30°角的直角三角板 ABC按如图方式放置(∠ABC=30°),其中 A,B 两点分别落在直线 m,n 上,若∠1=20°,则∠2 的度数为( )A.20° B.30° C.45° D.50°8.(4 分)(2024•宁波)若一组数据 2,3,x,5,7 的众数为 7,则这组数据的中位数为( )A.2B.3C.5D.79.(4 分)(2024•宁波)如图,在 Rt△ABC 中,∠A=90°,BC=2,以 BC 的中点 O 为圆心⊙O 分别与 AB,AC 相切于 D,E 两点,则的长为( )A.B.C.πD.2π10.(4 分)(2024•宁波)抛物线 y=x22x﹣+m2+2(m 是常数)的顶点在( )A.第一象限B.第二象限C.第三象限D.第四象限11.(4 分)(2024•宁波)如图,四边形 ABCD 是边长为 6 的正方形,点 E 在边 AB 上,BE=4,过点 E 作 EF∥BC,分别交 BD,CD 于 G,F 两点.若 M,N 分别是 DG,CE 的中点,则 MN 的长为( )A.3B.C.D.412.(4 分)(2024•宁波)一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形,在满足条件的所有分割中.若知道九个小矩形中 n 个小矩形的周长,就一定能算出这个大矩形的面积,则 n 的最小值是( )A.3B.4C.5D.6 二、填空题(每题 4 分,满分 24 分,将答案填在答题纸上)13....