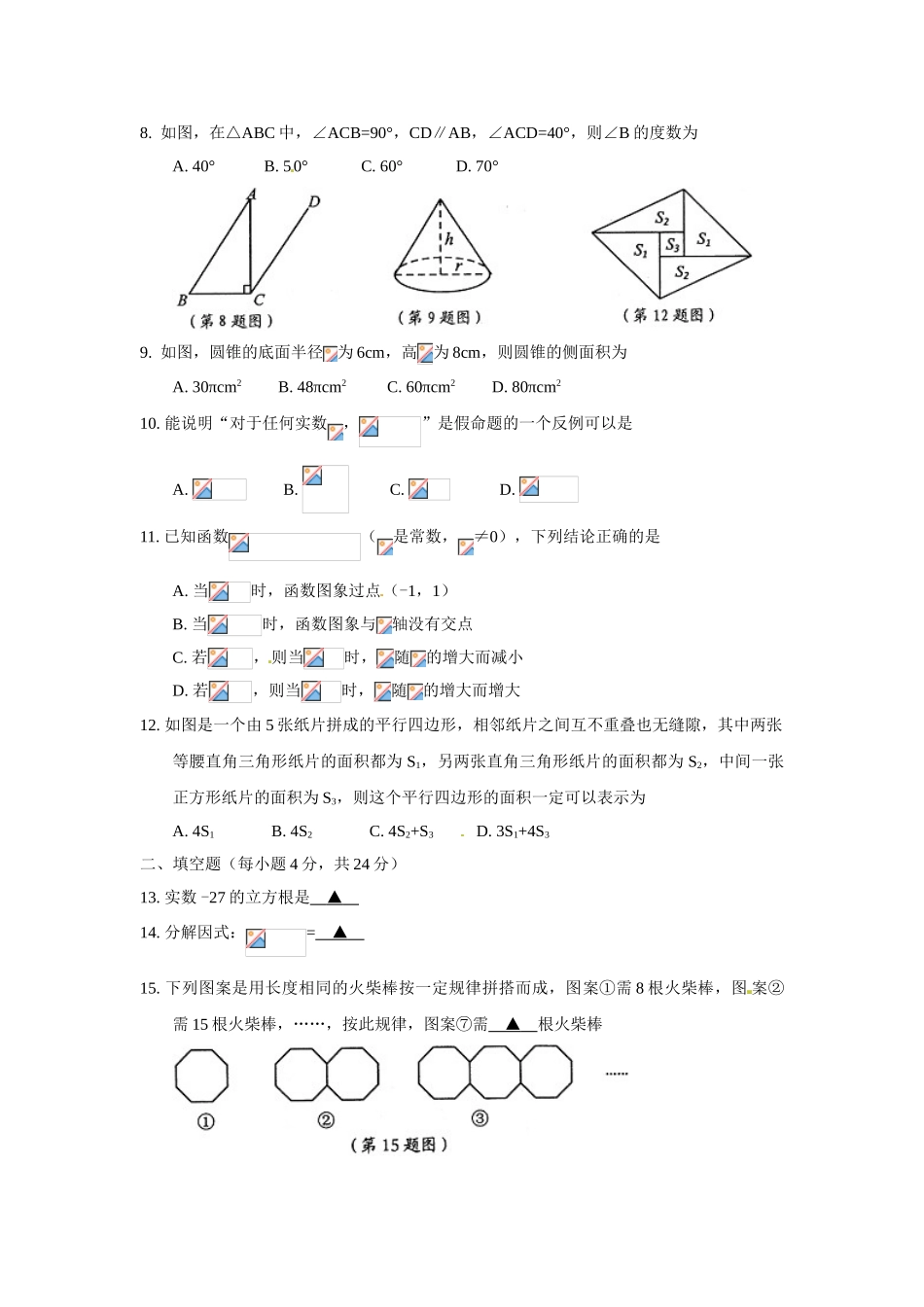
宁波市 2024 年初中毕业生学业考试数 学 试 题满分 150 分,考试时间 120 分钟一、选择题(每小题 4 分,共 48 分,在每小题给出的四个选项中, 只有一项符合题目要求)1. 6 的相反数是A. -6 B. C. D. 62. 下列计算正确的是A. B. C. D. 3. 宁波栎社国际机场三期扩建工程建设总投资 84.5 亿元,其中 84.5 亿元用科学计数法表示为A. 0.845×1010元 B. 84.5×108元 C. 8.45×109元 D. 8.45×1010元4. 使二次根式有意义的的取值范围是A. B. C. D. 5. 如图所示的几何体的主视图为6. 一个不透明布袋里装 有 1 个白球、2 个黑球、3 个红球,它们除颜色外都相同。从中任意摸出一个球,是红球的概率为A. B. C. D. 7. 某班 10 名学生校服尺寸与对应人数如下表所示:尺寸(cm)160165170175180学生人数(人)13222则这 10 名学生校服尺寸的众数和中位数分别为A. 165cm,165cm B. 165cm,170cm C. 170cm,165cm D. 170cm,170cm8. 如图,在△ABC 中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B 的度数为A. 40° B. 50° C. 60° D. 70°9. 如图,圆锥的底面半径为 6cm,高为 8cm,则圆锥的侧面积为A. 30πcm2 B. 48πcm2 C. 60πcm2 D. 80πcm210. 能说明“对于任何实数,”是假命题的一个反例可以是A. B. C. D. 11. 已知函数(是常数,≠0),下列结论正确的是A. 当时,函数图象过点(-1,1)B. 当时,函数图象与轴没有交点C. 若,则当时,随的增大而减小D. 若,则当时,随的增大而增大12. 如图是一个由 5 张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为 S1,另两张直角三角形纸片的面积都为 S2,中间一张正方形纸片的面积为 S3,则这个平行四边形的面积一定可以表示为A. 4S1 B. 4S2 C. 4S2+S3 D. 3S1+4S3 二、填空题(每小题 4 分,共 24 分)13. 实数 -27 的立方根是 ▲ 14. 分解因式:= ▲ 15. 下列图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需 8 根火柴棒,图 案②需 15 根火柴棒,……,按此规律,图案⑦需 ▲ 根火柴棒16. 如图,在一次数学课外实践活动中,小聪在距离旗杆 10m 的 A 处测得旗杆顶端 B 的仰角为 60°,测角仪高 AD 为 1m,则旗杆高 BC 为 ▲ m(结果保留根号)17. 如图,半圆 O 的直径 AB=2,弦 CD∥AB,∠COD=90°,则...