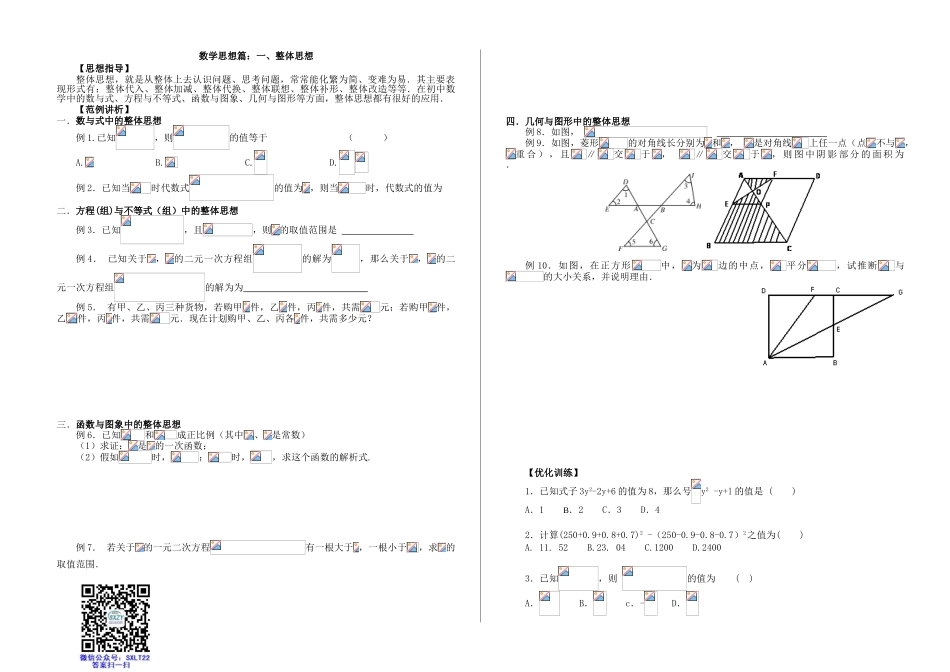
数学思想篇:一、整体思想【思想指导】整体思想,就是从整体上去认识问题、思考问题,常常能化繁为简、变难为易.其主要表现形式有:整体代入、整体加减、整体代换、整体联想、整体补形、整体改造等等.在初中数学中的数与式、方程与不等式、函数与图象、几何与图形等方面,整体思想都有很好的应用.【范例讲析】一.数与式中的整体思想例 1.已知,则的值等于 ( )A. B. C. D.例 2.已知当时代数式的值为 ,则当时,代数式的值为 二.方程(组)与不等式(组)中的整体思想例 3.已知,且,则的取值范围是 例 4. 已知关于,的二元一次方程组的解为,那么关于,的二元一次方程组的解为为 例 5. 有甲、乙、丙三种货物,若购甲 件,乙件,丙 件,共需元;若购甲件,乙件,丙 件,共需元.现在计划购甲、乙、丙各 件,共需多少元?三.函数与图象中的整体思想例 6.已知和成正比例(其中、是常数)(1)求证:是的一次函数;(2)假如时,;时,,求这个函数的解析式.例 7. 若关于的一元二次方程有一根大于 ,一根小于,求的取值范围.四.几何与图形中的整体思想例 8.如图, 例 9.如图,菱形的对角线长分别为 和, 是对角线上任一点(点不与,重 合 ) , 且∥交于, ∥交于, 则 图 中 阴 影 部 分 的 面 积 为 .例 10.如图,在正方形中,为边的中点,平分,试推断与的大小关系,并说明理由. 【优化训练】1.已知式子 3y2-2y+6 的值为 8,那么号y2 -y+l 的值是 ( )A.1 B.2 C.3 D.42.计算(250+0.9+0.8+0.7)2 -(250-0.9-0.8-0.7)2之值为( )A. 11. 52 B.23. 04 C.1200 D.24003.已知,则 的值为 ( )A. B. c.- D.4.已知 a2-3a+1=0,则的值为 ( )A. 45 B. 46 C. 47 D. 485.如图,在梯形 ABCD 中,MN 是梯形的中位线,E 是 AD 上一点,若 S△EMN =4,则 S 梯形 ABCD= ( )A.8 B.12 C.16 D.206 . 已 知 al , a2 , … , a2024 均 为 正 数 , 且 满 足 M= ( al+a2+…+a2001 ) ( a2+a3+---+a2001-a2024),N=(al +a2+- +a200l -a2024)(a2 +a3+…+a2oo1),则 M 与 N 之间的关系是 ( )A.M>N B.M