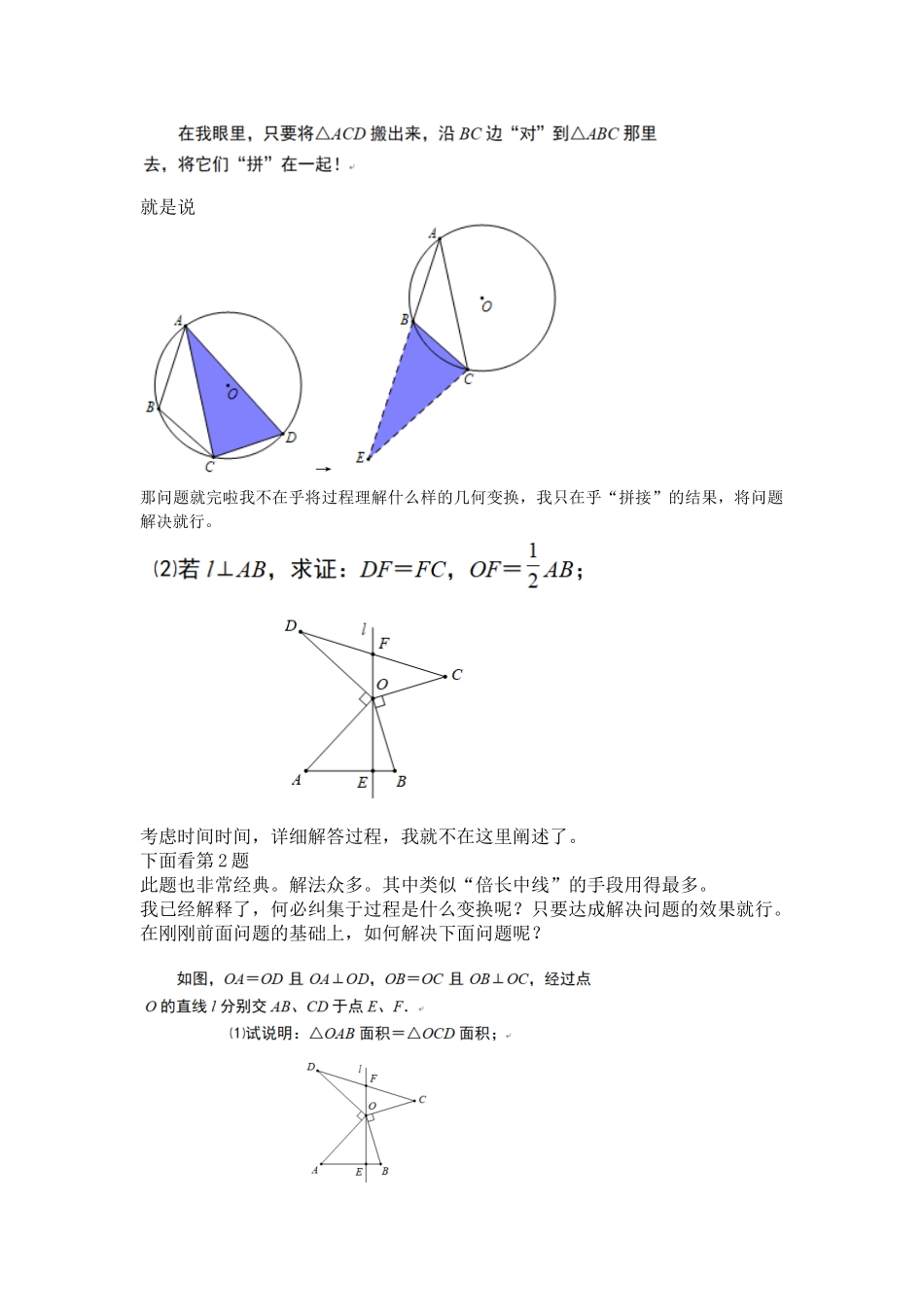
首先谈谈我对几何变换的认识就解决平面几何问题而言,觉得具体的辅助线,都可以通过传统的局部处理,如延长、作角相等、作平行、作垂直等等而实现。辅助线的添加似乎与几何变换扯不上关系。 但采纳几何变换的观点,从整体高度,更加容易看清图形之间的内在联系。粗糙地说,传统添加辅助线的方法有点“小家子气”,高度不够。在遇到较为困难的几何问题,要发现辅助线的添加,比较困难。而几何变换考虑图形之间的整体联系,更容易发现解决问题的关键所在。纵观最近几年各地中考试卷,对于一些问题的解决,假如不从变换的观点去分析思考,要发现问题的解决思路,则是相当困难的.另外,我们对几何变换有一种错觉,认为在“全等变换”中,“几何变换=平移+旋转+翻折”。其实,这样对“几何变换”的理解是不全面的,其实将一个几何图形任意拨动一下,都可以理解成是一次几何变换。我们这里主要讲全等变换,暂不想扯到相似变换。将所有复杂的变换分解,最后只有三种最基本的变换:平移、旋转、翻折。反之也是,你将平面上的图形任意拨动一下,其过程效果一定可以通过上述三种变换来完成,少一个肯定不行。下面干脆一些,还是讲题目吧。这样老师们听起来更加感性。此题网友们讨论比较多,各种解法也比较多。但对于我来说,我的理解是这样的。就是说→那问题就完啦我不在乎将过程理解什么样的几何变换,我只在乎“拼接”的结果,将问题解决就行。考虑时间时间,详细解答过程,我就不在这里阐述了。下面看第 2 题此题也非常经典。解法众多。其中类似“倍长中线”的手段用得最多。我已经解释了,何必纠集于过程是什么变换呢?只要达成解决问题的效果就行。在刚刚前面问题的基础上,如何解决下面问题呢?又如何解决下面问题呢?就是说,这个经典问题可以出现三个系列甚至更多小题。我的解法或许与大家的想法不是太相同。我考虑上下两个三角形,有两个角互补,又有边相同,所以我萌生将这两个三角形拼在一起的想法。事实上,这样一想,前面的问题可以全部解决。很有意思。请大家体会一下呢下面讲解第 3 道题目,这是一道“名题”印象中,这题目刚刚在网上出现时,许多人不会做,继而是“憎恶”这道题目,看了解答后,感觉这道题目太难了。其实我的理解与大家不同。我感觉我下面的想法还是比较自然的。我关注到了下面现象:即 DF=BE 要求 AE+AF 的最小值。我要想方设法“化折为直”显然图中那个状态,这两个线段的和怎么也不可能“拉直”的因此我...