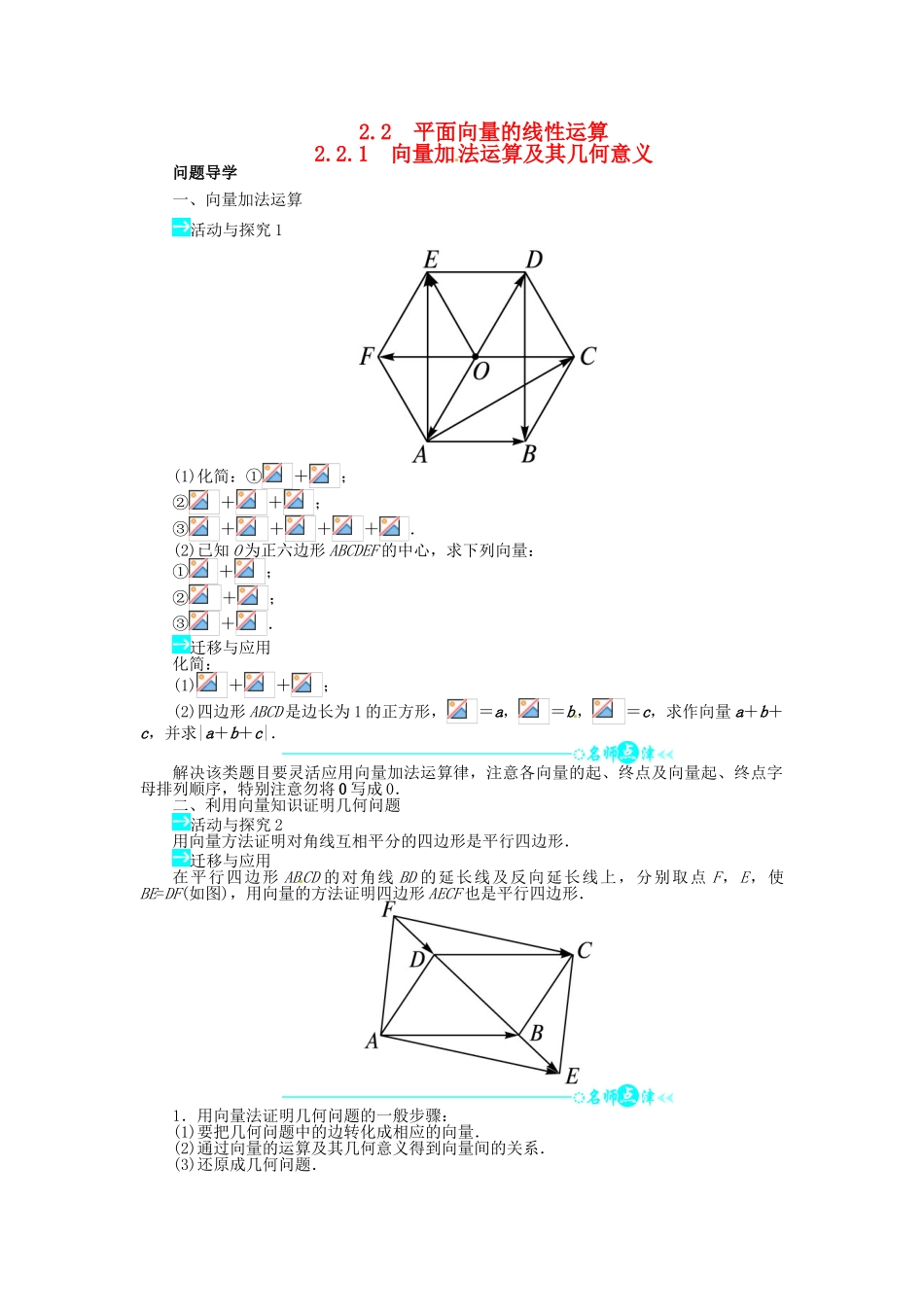
2.2 平面向量的线性运算2.2.1 向量加法运算及其几何意义问题导学一、向量加法运算活动与探究 1(1)化简:①+;②++;③++++.(2)已知 O 为正六边形 ABCDEF 的中心,求下列向量:①+;②+;③+.迁移与应用化简:(1)++;(2)四边形 ABCD 是边长为 1 的正方形,=a,=b,=c,求作向量 a+b+c,并求|a+b+c|.解决该类题目要灵活应用向量加法运算律,注意各向量的起、终点及向量起、终点字母排列顺序,特别注意勿将 0 写成 0.二、利用向量知识证明几何问题活动与探究 2用向量方法证明对角线互相平分的四边形是平行四边形.迁移与应用在平行四边形 ABCD 的对角线 BD 的延长线及反向延长线上,分别取点 F,E,使BE=DF(如图),用向量的方法证明四边形 AECF 也是平行四边形.1.用向量法证明几何问题的一般步骤:(1)要把几何问题中的边转化成相应的向量.(2)通过向量的运算及其几何意义得到向量间的关系.(3)还原成几何问题.2.注意以下两个问题:(1)法则的灵活应用.(2)要注意有向线段表示的向量相等,说 明有向线段所在直线平行或重合且线段的长度相等.三、向量加法的实际应用活动与探究 3在四川汶川“5·12”大地震后,一架救援直升飞机从 A 地沿北偏东 60°方向飞行了40 km 到达 B 地,再由 B 地沿正北方向飞行 40 km 到达 C 地,求此时直升飞机与 A 地的相对位置.迁移与应用在长江某渡口上,江水以 2 km/h 的速度向东流,长江南岸的一艘渡船的速度为 2 km/h,要使渡船渡江的时间最短,求渡船实际航行的速度的大小和方向.向量应用题要首先画出图形.解决的步骤是:(1)将应用问题中的量抽象成向量;(2)化归为向量问题,进行向量运算;(3)将向量问题还原为实际问题.当堂检测1.在四边形 ABCD 中,=+,则( )A.ABCD 一定是矩形B.ABCD 一定是菱形C.ABCD 一定是正方形D.ABCD 一定是平行四边形2.+++++=( )A.0 B.0C.2 D.-23.下列等式不成立的是( )A.0+a=a B.a+b=b+aC.+=2 D.+=4.化简(+)+(+)+=__________.5.若 a=“向北走 8 km”,b=“向东走 8 km”,则|a+b|=__________;a+b 的方向是__________. 提示:用最精炼的语言把你当堂掌握的核心知识的精华部分和基本技能的要领部分写下来并进行识记.答案:课前预习导学【预习导引】1.两个向量和2.和 a+b a+b 三角形法则3.平行四边形法则4.b+a (a+b)+c a+(b...