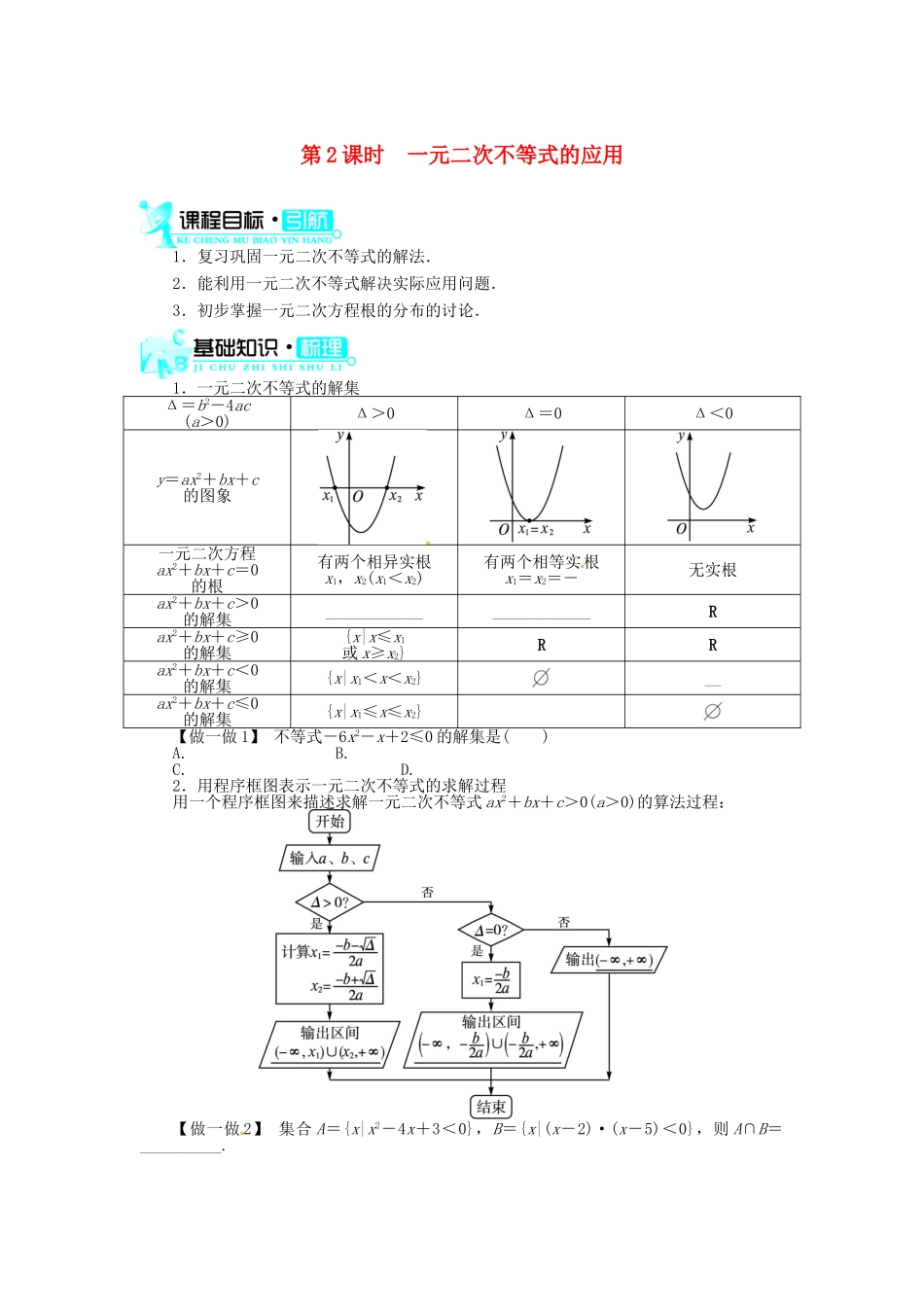
第 2 课时 一元二次不等式的应用1.复习巩固一元二次不等式的解法.2.能利用一元二次不等式解决实际应用问题.3.初步掌握一元二次方程根的分布的讨论.1.一元二次不等式的解集Δ=b2-4ac(a>0)Δ>0Δ=0Δ<0y=ax2+bx+c的图象一元二次方程ax2+bx+c=0的根有两个相异实根x1,x2(x1<x2)有两个相等实根x1=x2=-无实根ax2+bx+c>0的解集________________________Rax2+bx+c≥0的解集{x|x≤x1或 x≥x2}RRax2+bx+c<0的解集{x|x1<x<x2}__ax2+bx+c≤0的解集{x|x1≤x≤x2}【做一做 1】 不等式-6x2-x+2≤0 的解集是( )A.B.C.D.2.用程序框图表示一元二次不等式的求解过程用一个程序框图来描述求解一元二次不等式 ax2+bx+c>0(a>0)的算法过程:【做一做 2】 集合 A={x|x2-4x+3<0},B={x|(x-2)·(x-5)<0},则 A∩B=__________.答案:1. 【做一做 1】 B【做一做 2】 {x|2<x<3}一元二次方程的根的分布讨论剖析:关于 x 的一元二次方程 ax2+bx+c=0(a≠0),判别式 Δ=b2-4ac.(1)定理 1:方程没有实数根Δ<0.定理 2:方程有两个相等的实数根Δ=0.定理 3:方程有两个不相等的实数根Δ>0.定理 4:方程有实数根Δ≥0.(2)设一元二次方程的两个实根为 x1,x2,且 x1≤x2.定理 5:x1>0,x2>0定理 6:x1<0,x2<0定理 7:x1<0<x2<0.定理 8:x1=0,x2>0c=0 且<0;x1<0,x2=0c=0 且>0.题型一 求参数的取值范围【例题 1】 关于 x 的一元二次方程 x2-mx+m=0 没有实数根,求实数 m 的取值范围.分析:根据一元二次方程 x2-mx+m=0 没有实数根列出 m 满足的条件(一元二次不等式),解不等式得到实数 m 的取值范围.反思:已知一元二次方程的根的分布求参数的取值范围的步骤:(1)利用一元二次方程根的分布情况列出参数满足的条件——不等式(组);(2)解不等式(组)得参数的取值范围.题型二 实际应用题【例题 2】 政府收购某种农产品的原价是 100 元/担,其中征税标准为每 100 元征 10元(叫做税率为 10 个百分点,即 10%),计划收购 a 万担;为了减轻农民的负担,现决定 将税率降低 x 个百分点,预计收购量可增加 2x 个百分点.要使此项税收在税率调节后不低于原计划的 83.2%,试确定 x 的取值范围.分析:税收=征税总额×税率,先建立税收随税率降低的百分点 x 变化的函数关系,再用不等式表示不等关系即可.反思:解不等式应用题,...