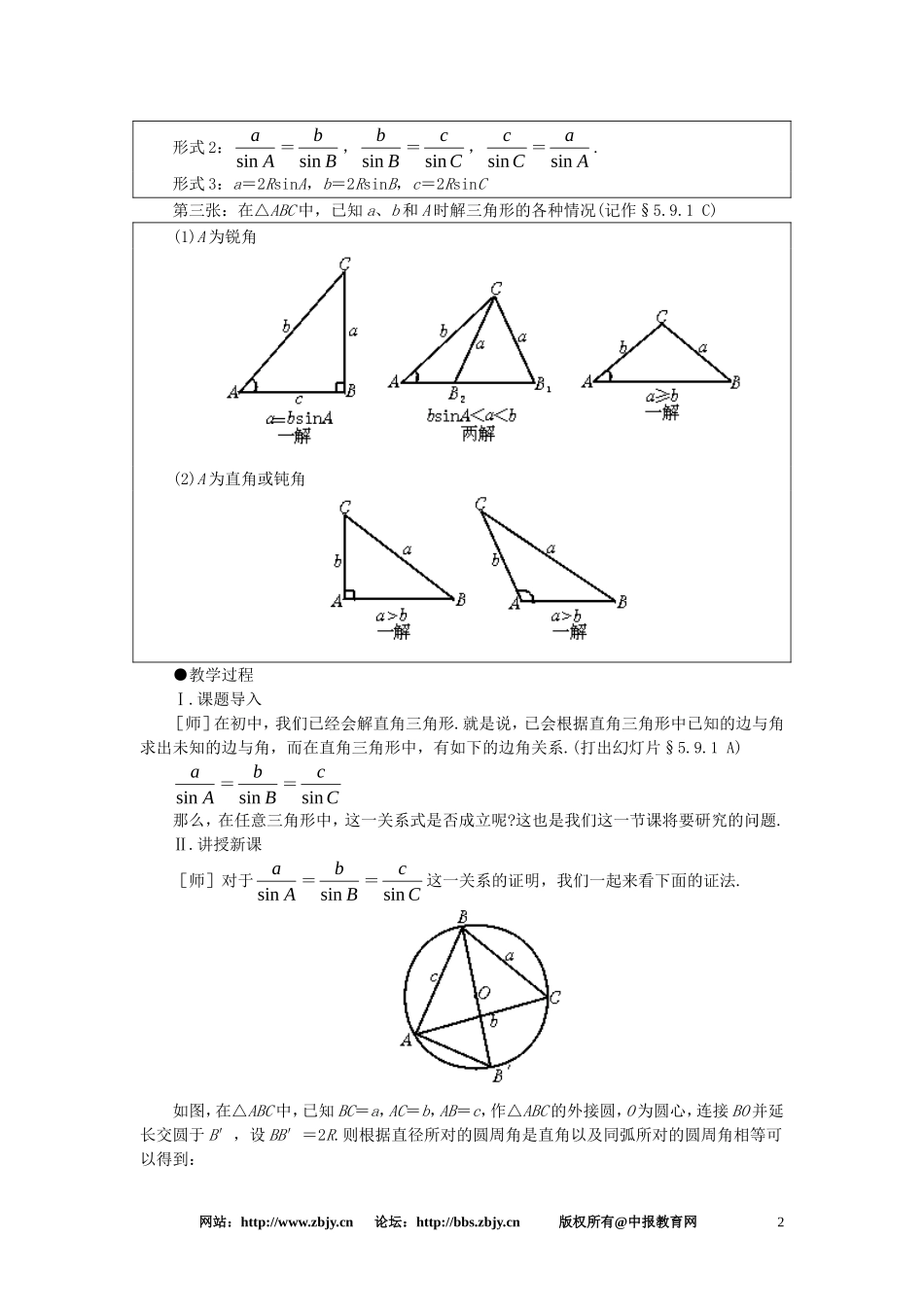
●课题§5.9.1 正弦定理、余弦定理(一)●教学目标(一)知识目标正弦定理.(二)能力目标1.了解向量知识应用;2.掌握正弦定理推导过程;3.会利用正弦定理证明简单三角形问题;4.会利用正弦定理求解简单斜三角形边角问题;5.能利用计算器进行运算.(三)德育目标通过三角函数、正弦定理、向量数量积等多处知识间联系来体现事物之间的普遍联系与辩证统一.●教学重点正弦定理证明及应用.●教学难点1.向量知识在证明正弦定理时的应用,与向量知识的联系过程;2.正弦定理在解三角形时应用思路.●教学方法启发引导式1.引导学生在证明正弦定理时与向量数量积的知识产生联系,主要在于如何与角产生联系,并注意利用三角函数的诱导公式对同角正余弦进行转化,在应用向量知识的同时,体现三角函数、正弦定理、向量数量积等多处知识之间的联系.2.启发学生注意正弦定理的变形式,并总结正弦定理的适用题型的特点,在恰当时机正确选用正弦定理达到求解、求证目的.●教具准备投影仪、幻灯片三张第一张:直角三角形边角关系(记作§5.9.1 A)在 Rt△ABC 中,已知 BC=a,AC=b,AB=c,则有sinA= ca ,sinB= cb ,sinC=1,即 c=Aasin,c=Bbsin,c=Ccsin,∴Aasin=Bbsin=Ccsin第二张:正弦定理(记作§5.9.1 B)形式 1:Aasin=Bbsin=Ccsin=2R网站:http://www.zbjy.cn 论坛:http://bbs.zbjy.cn 版权所有@中报教育网1形式 2:Aasin=Bbsin,Bbsin=Ccsin,Ccsin=Aasin.形式 3:a=2RsinA,b=2RsinB,c=2RsinC第三张:在△ABC 中,已知 a、b 和 A 时解三角形的各种情况(记作§5.9.1 C)(1)A 为锐角(2)A 为直角或钝角●教学过程Ⅰ.课题导入[师]在初中,我们已经会解直角三角形.就是说,已会根据直角三角形中已知的边与角求出未知的边与角,而在直角三角形中,有如下的边角关系.(打出幻灯片§5.9.1 A)Aasin=Bbsin=Ccsin 那么,在任意三角形中,这一关系式是否成立呢?这也是我们这一节课将要研究的问题.Ⅱ.讲授新课[师]对于Aasin=Bbsin=Ccsin这一关系的证明,我们一起来看下面的证法.如图,在△ABC 中,已知 BC=a,AC=b,AB=c,作△ABC 的外接圆,O 为圆心,连接 BO 并延长交圆于 B′,设 BB′=2R.则根据直径所对的圆周角是直角以及同弧所对的圆周角相等可以得到:网站:http://www.zbjy.cn 论坛:http://bbs.zbjy.cn 版权所有@中报教育网2∠BAB′=90°,∠C=∠B′∴sinC=sinB′= Rc2∴Ccsin=2R同理可得Aasin...