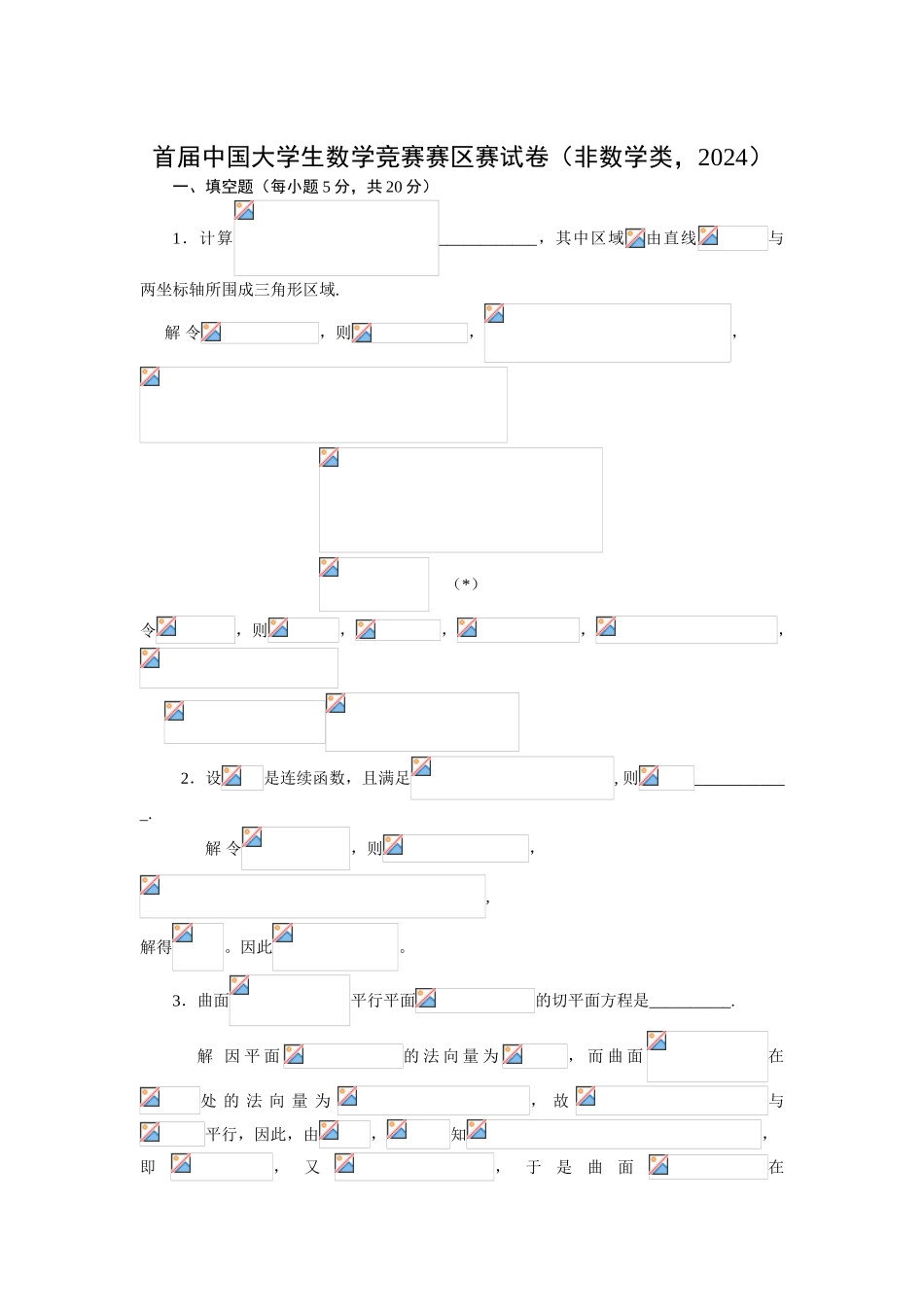
首届中国大学生数学竞赛赛区赛试卷(非数学类,2024)一、填空题(每小题 5 分,共 20 分)1.计算____________,其中区域由直线与两坐标轴所围成三角形区域.解 令,则,, (*)令,则,,,,2.设是连续函数,且满足, 则____________.解 令,则,,解得。因此。3.曲面平行平面的切平面方程是__________.解 因 平 面的 法 向 量 为, 而 曲 面在处 的 法 向 量 为, 故与平行,因此,由,知,即,又,于是曲面在处 的 切 平 面 方 程 是, 即 曲 面平行平面的切平面方程是。4.设函数由方程确定,其中具有二阶导数,且,则________________.解 方程的两边对求导,得因,故,即,因此不会:二、(5 分)求极限,其中是给定的正整数.解法 1 因故因此解法 2 因故三、(15 分)设函数连续,,且,为常数,求并讨论在处的连续性.解 由和函数连续知,因,故,因此,当时,,故当时,,这表明在处连续.四、(15 分)已知平面区域,为的正向边界试证:(1);(2).证 因被积函数的偏导数连续在上连续,故由格林公式知(1)而关于和是对称的,即知因此(2)因故由知即五、(10 分)已知,,是某二阶常系数线性非齐次微分方程的三个解,试求此微分方程.解 设,,是二阶常系数线性非齐次微分方程的三个解,则和都是二阶常系数线性齐次微分方程的解,因此的特征多项式是,而的特征多项式是因此二阶常系数线性齐次微分方程为,由和,知,二阶常系数线性非齐次微分方程为六、(10 分)设抛物线过原点.当时,,又已知该抛物线与轴及直线所围图形的面积为.试确定,使此图形绕轴旋转一周而成的旋转体的体积最小.解 因抛物线过原点,故,于是即而此图形绕轴旋转一周而成的旋转体的体积即令,得即因此,,.七、(15 分)已知满足, 且, 求函数项级数之和.解 ,即由一阶线性非齐次微分方程公式知即因此由知,,于是下面求级数的和:令则即由一阶线性非齐次微分方程公式知令,得,因此级数的和八、(10 分)求时, 与等价的无穷大量.解 令,则因当,时,,故在上严格单调减。因此即,又,,所以,当时, 与等价的无穷大量是。