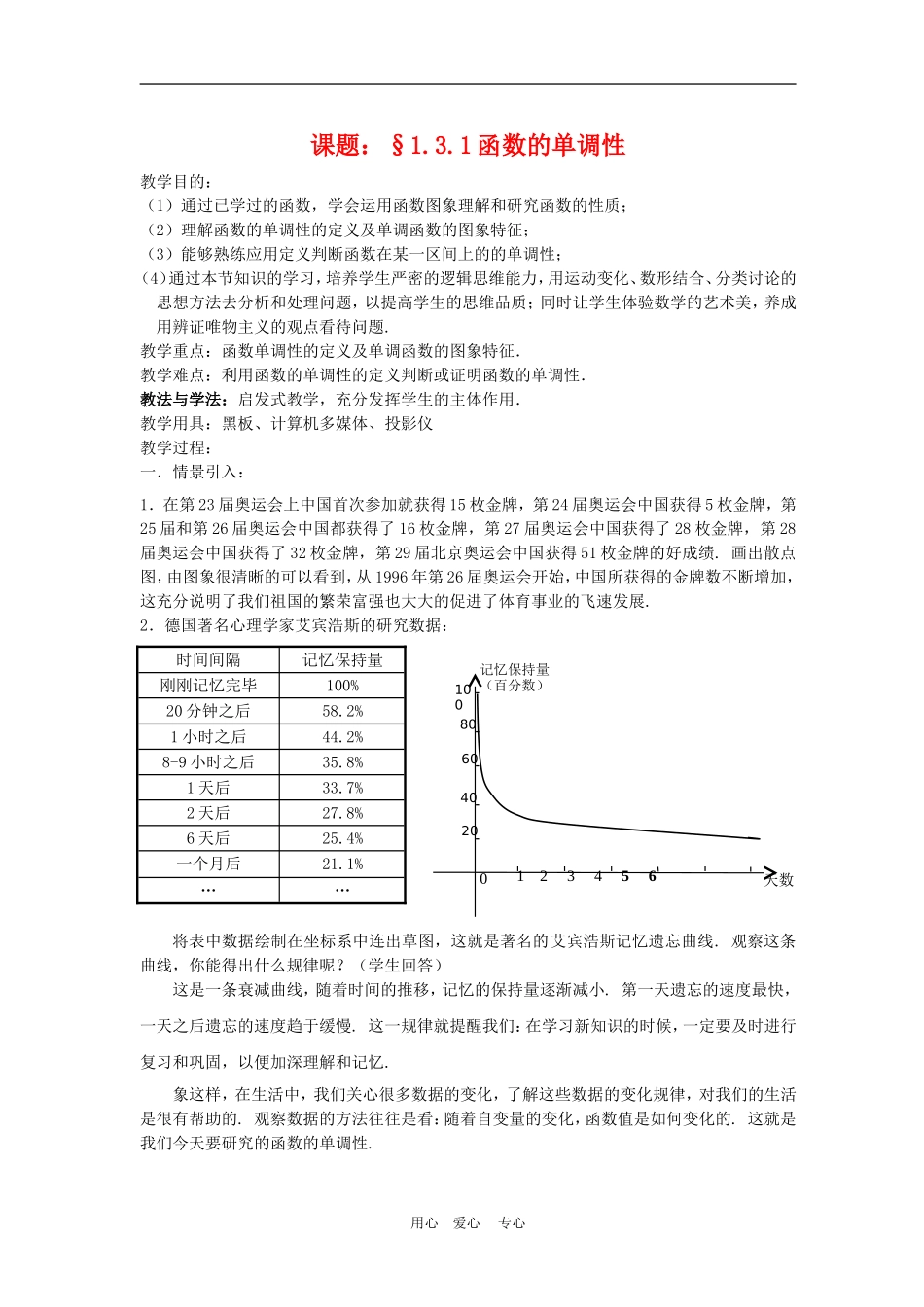
课题:§1.3.1 函数的单调性教学目的:(1)通过已学过的函数,学会运用函数图象理解和研究函数的性质; (2)理解函数的单调性的定义及单调函数的图象特征;(3)能够熟练应用定义判断函数在某一区间上的的单调性;(4)通过本节知识的学习,培养学生严密的逻辑思维能力,用运动变化、数形结合、分类讨论的思想方法去分析和处理问题,以提高学生的思维品质;同时让学生体验数学的艺术美,养成用辨证唯物主义的观点看待问题.教学重点:函数单调性的定义及单调函数的图象特征.教学难点:利用函数的单调性的定义判断或证明函数的单调性.教法与学法:启发式教学,充分发挥学生的主体作用. 教学用具:黑板、计算机多媒体、投影仪教学过程:一.情景引入:1.在第 23 届奥运会上中国首次参加就获得 15 枚金牌,第 24 届奥运会中国获得 5 枚金牌,第25 届和第 26 届奥运会中国都获得了 16 枚金牌,第 27 届奥运会中国获得了 28 枚金牌,第 28届奥运会中国获得了 32 枚金牌,第 29 届北京奥运会中国获得 51 枚金牌的好成绩. 画出散点图,由图象很清晰的可以看到,从 1996 年第 26 届奥运会开始,中国所获得的金牌数不断增加,这充分说明了我们祖国的繁荣富强也大大的促进了体育事业的飞速发展.2.德国著名心理学家艾宾浩斯的研究数据:时间间隔记忆保持量刚刚记忆完毕100%20 分钟之后58.2%1 小时之后44.2%8-9 小时之后35.8%1 天后33.7%2 天后27.8%6 天后25.4%一个月后21.1%……将表中数据绘制在坐标系中连出草图,这就是著名的艾宾浩斯记忆遗忘曲线. 观察这条曲线,你能得出什么规律呢?(学生回答) 这是一条衰减曲线,随着时间的推移,记忆的保持量逐渐减小. 第一天遗忘的速度最快,一天之后遗忘的速度趋于缓慢. 这一规律就提醒我们:在学习新知识的时候,一定要及时进行复习和巩固,以便加深理解和记忆.象这样,在生活中,我们关心很多数据的变化,了解这些数据的变化规律,对我们的生活是很有帮助的. 观察数据的方法往往是看:随着自变量的变化,函数值是如何变化的. 这就是我们今天要研究的函数的单调性. 用心 爱心 专心天数记忆保持量(百分数)401 2 3 4 5 62060801000二.学习新课:观察下列函数的图象,回答当自变量 x 的值增加时,函数值 f(x)是如何变化的?(学生回答)(1)函数( )1f xx 的图象从左到右上升,即当 x 增大时 f(x) 随着增大,所以称函数1( )xf x ...