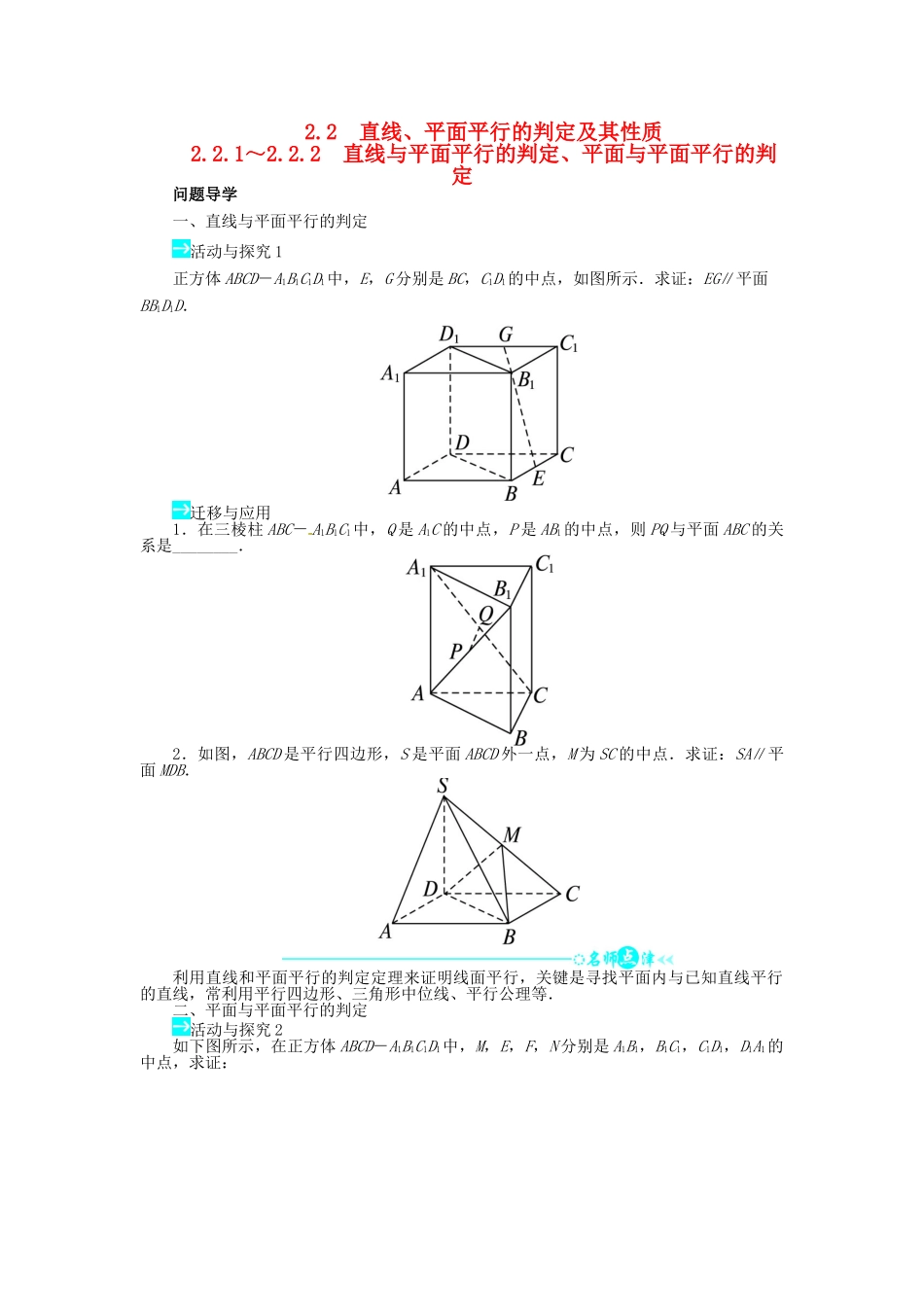
2.2 直线、平面平行的判定及其性质2.2.1~2.2.2 直线与平面平行的判定、平面与平面平行的判定问题导学一、直线与平面平行的判定活动与探究 1正方体 ABCD-A1B1C1D1中,E,G 分别是 BC,C1D1的中点,如图所示.求证:EG∥平面BB1D1D.迁移与应用1.在三棱柱 ABC- A1B1C1中,Q 是 A1C 的中点,P 是 AB1的中点,则 PQ 与平面 ABC 的关系是________.2.如图,ABCD 是平行四边形,S 是平面 ABCD 外一点,M 为 SC 的中点.求证:SA∥平面 MDB.利用直线和平面平行的判定定理来证明线面平行,关键是寻找平面内与已知直线平行的直线,常利用平行四边形、三角形中位线、平行公理等.二、平面与平面平行的判定活动与探究 2如下图所示,在正方体 ABCD-A1B1C1D1中,M,E,F,N 分别是 A1B1,B1C1,C1D1,D1A1的中点,求证:(1)E,F,B,D 四点共面;(2)平面 MAN∥平面 EFDB.迁移与应用1.已知三棱锥 P-ABC,D,E,F 分别是棱 PA,PB,PC 的中点,则面 DEF 与面 ABC 的位置关系是__________.2.已知四棱锥 P-ABCD 中,底面 ABCD 为平行四边形,点 M,N,Q 分别在 PA,BD,PD上,且 PM∶MA=BN∶ND=PQ∶QD.求证:平面 MNQ∥平面 PBC.两平面平行的判定定理是判定两平面平行的重要方法,在应用时,设法在一个平面内找两条相交直线与另一个平面平行.可以利用平行四边形、三角形中位线及平行公理等得到平行线.三、线面平行与面面平行的综合活动与探究 3已知正方体 ABCD-A1B1C1D1 中,E,F 分别是 AA1,CC1 的中点,求证:平面 BDF∥平面B1D1E.迁移与应用在 三 棱 柱 ABC - A1B1C1 中 , D 为 BC 边 上 的 中 点 , D1 为 B1C1 边 上 的 中 点 , 连 接AD,DC1,A1B,AC1,A1D1,BD1.求证:平面 A1BD1∥平面 ADC1.线线、线面、面面平行的判定关系可用下图示意:当堂检测1.能保证直线 a 与平面 α 平行的条件是( )A.a⊄α,b⊂α,a∥bB.b⊂α,a∥bC.b⊂α,c∥α,a∥b,a∥cD.b⊂α,A∈a,B∈a,C∈b,D∈b,且 AC=BD2.若 a,b,c,d 是直线,α,β 是平面,且 a,b⊂α;c,d⊂β,且 a∥c,b∥d,则平面 α 与平面 β( )A.平行 B.相交C.异面 D.不能确定3.已知平面 α 外不共线的三点 A,B,C 到平面 α 的距离都相等,则平面 α 与平面ABC 的位置关系是( )A.平行 B.相交C.平行或相交 D.以上均不正确4....