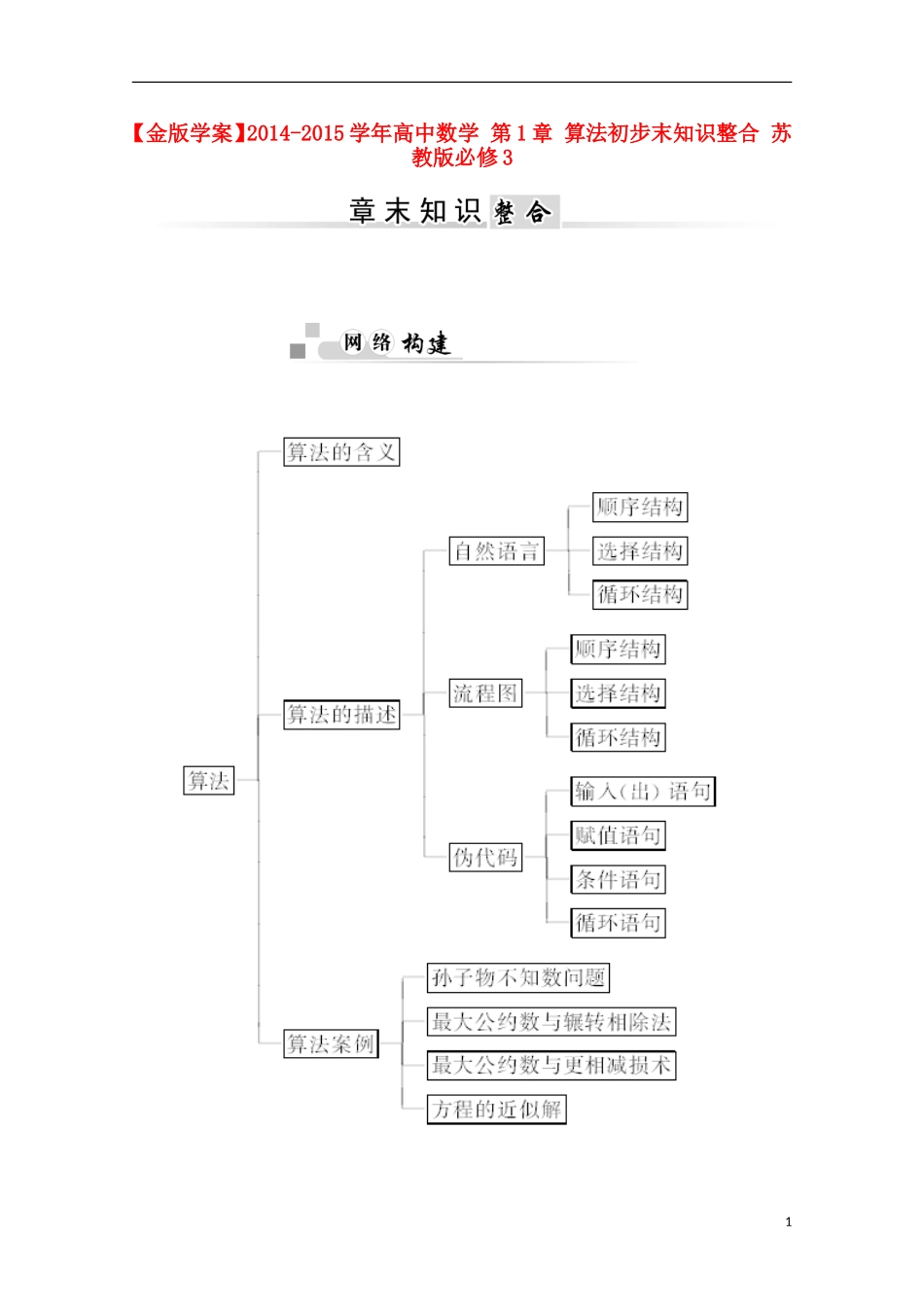
【金版学案】2014-2015 学年高中数学 第 1 章 算法初步末知识整合 苏教版必修 31 已知平面直角坐标系内两不同点 A,B,试求 AB 的垂直平分线的方程.试写出这个问题的算法.分析:首先应判断 A、B 两点的横、纵坐标是否相等,在不等时,先求垂直平分的斜率或线段 AB 的中点坐标,最后由点斜式写出直线方程.解析:算法如下:S1 输入 x1,y1,x2,y2.S2 判断 x1=x2是否成立.如果成立,则输出所求的直线方程为 y←,转结束;如果不成立,则判断 y1=y2是否成立.如果成立,则输出所求的直线方程为 x←,转结束;如果不成立,则输出所求的直线方程为 y-=-,转结束.S3 结束.规律总结:算法设计与一般意义上的解决问题不同,这是一类问题的一般解法的抽象与概括,它要借助一般的问题解决方法,又要包含这类问题的所有可能情形,它往往是把问题的解法划分为若干个可执行的步骤,有时甚至是重复多次,但最终都必须在有限个步骤之内完成.变式训练1.设计一个算法,将高一某班 50 名同学某次数学考试成绩不及格者的分数打印出来.解析:算法步骤如下:S1 令 n←1;S2 如果 n>50,则转到 S7;S3 输入一个学生的成绩 G;S4 将 G 和 60 比较,如果 G<60,则输出 G;S5 n←n+1;S6 转到 S2;S7 结束.22.已知平面直角坐标系中的两点 A(-1,0),B(3,2),写出求线段 AB 的垂直平分线方程的一个算法.解析:算法步骤如下:S1 计算 x0==1,y0==1,得 AB 的中点 N(1,1);S2 计算 k1==,得 AB 的斜率;S3 计算 k=-=-2,得 AB 垂直平分线的斜率;S4 得直线 AB 垂直平分线的方程 y-1=-2(x-1),即 y=-2x+3,输出. 求正数 a 平方根近似值的一种算法思路是这样的:第一步 确定平方根的首次近似值:a1 (a1可以任取一个正数);第二步 由代数式 b1=求出 b1;第三步 取二者的算术平均值 a2=为第二次近似值;第四步 由方程 b2=求出 b2 ;第五步 取算术平均值 a3=作为第三次近似值;……反复进行上述步骤,直到获得满足误差在 0.1 以内的数为止.请依照上述思路,画出相应的算法流程图.解析:流程图如下:3规律总结:流程图是用规定的图形和流程线来准确、直观、形象地表示算法的图形.画流程图之前应先对问题设计出合理有效的算法,然后分析算法的逻辑结构,根据逻辑结构画出相应的流程图.变式训练3.写出解方程 ax+b=0(a,b 为常数)的算法...