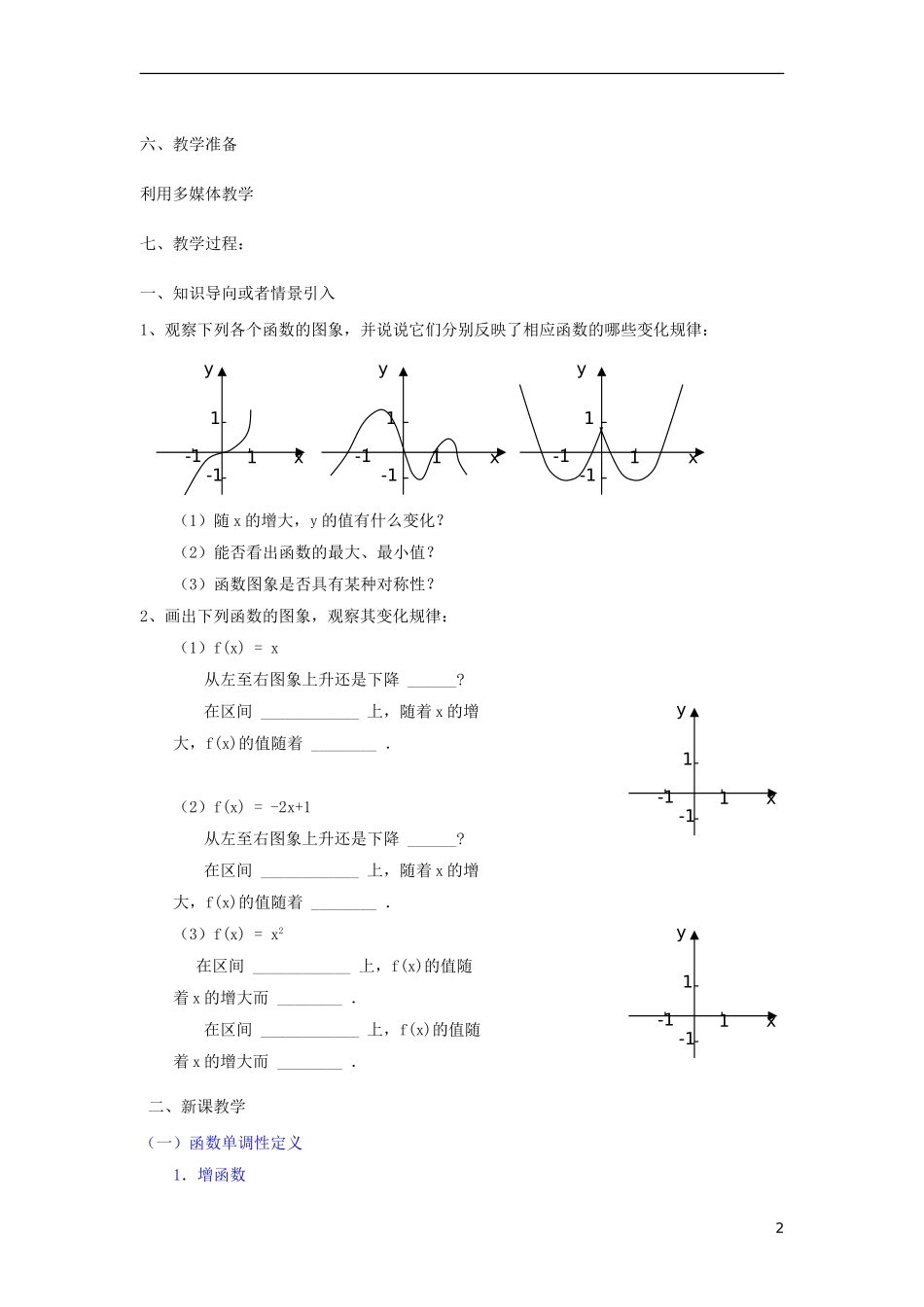
函数的单调性与最大(小)值教材分析本课时主要学习函数的单调性的概念,依据函数图象判断函数的单调性和依据定义证明函数的单调性。本节课是在学生学习了函数概念的基础上所研究的函数的一个重要性质。函数单调性的概念是研究具体函数函数单调性的依据,在研究函数的值域、定义域、最值等性质中有重要应用。函数单调性的研究方法也具有典型意义,对加强“数”与“形”的结合,由直观到抽象;由特殊到一般的研究方法有很大帮助。掌握本节内容不仅为今后的函数学习打下理论基础,还有利于培养学生的抽象思维能力,及分析问题和解决问题的能力二、教学目标1、知识与技能目标(1)使学生理解函数单调性的概念,并能判断一些简单函数在给定区间上的单调性。(2)启发学生发现问题和提出问题,培养学生分析问题、认识问题和解决问题的能力。(3)通过观察-猜想-推理-证明这一个重要的思想方法,进一步培养学生的逻辑推理能力和创新意识。 2、过程与方法目标 (1)通过渗透数形结合的数学思想,对学生进行辨证唯物主义的思想教育。 (2)探究与活动,明白考虑问题要细致,说理要明确。3、情感态度与价值观目标:学生通过一系列丰富的数学活动,培养观察能力,归纳总结能力,加深对数形结合思想的理解。三、教学重点函数的单调性、最大(小)值及其几何意义,四、教学难点利用函数的单调性定义判断、证明函数的单调性,利用函数的单调性求函数的最大(小)值五、教学策略在教法学法方面,采用启发式、探讨式的教学方法,引导学生自主探究,合作交流。通过学生身边熟悉的事物,教师创造疑问,学生想办法解决疑问,通过教师的启发点拨,学生以自己的努力找到了解决问题的方法。1六、教学准备利用多媒体教学七、教学过程:一、知识导向或者情景引入1、观察下列各个函数的图象,并说说它们分别反映了相应函数的哪些变化规律:(1)随 x 的增大,y 的值有什么变化?(2)能否看出函数的最大、最小值?(3)函数图象是否具有某种对称性?2、画出下列函数的图象,观察其变化规律:(1)f(x) = x 从左至右图象上升还是下降 ______? 在区间 ____________ 上,随着 x 的增大,f(x)的值随着 ________ .(2)f(x) = -2x+1 从左至右图象上升还是下降 ______? 在区间 ____________ 上,随着 x 的增大,f(x)的值随着 ________ .(3)f(x) = x2在区间 ____________ 上,f(x)的值随着 x 的增大而 ________ . 在区间 ____________...