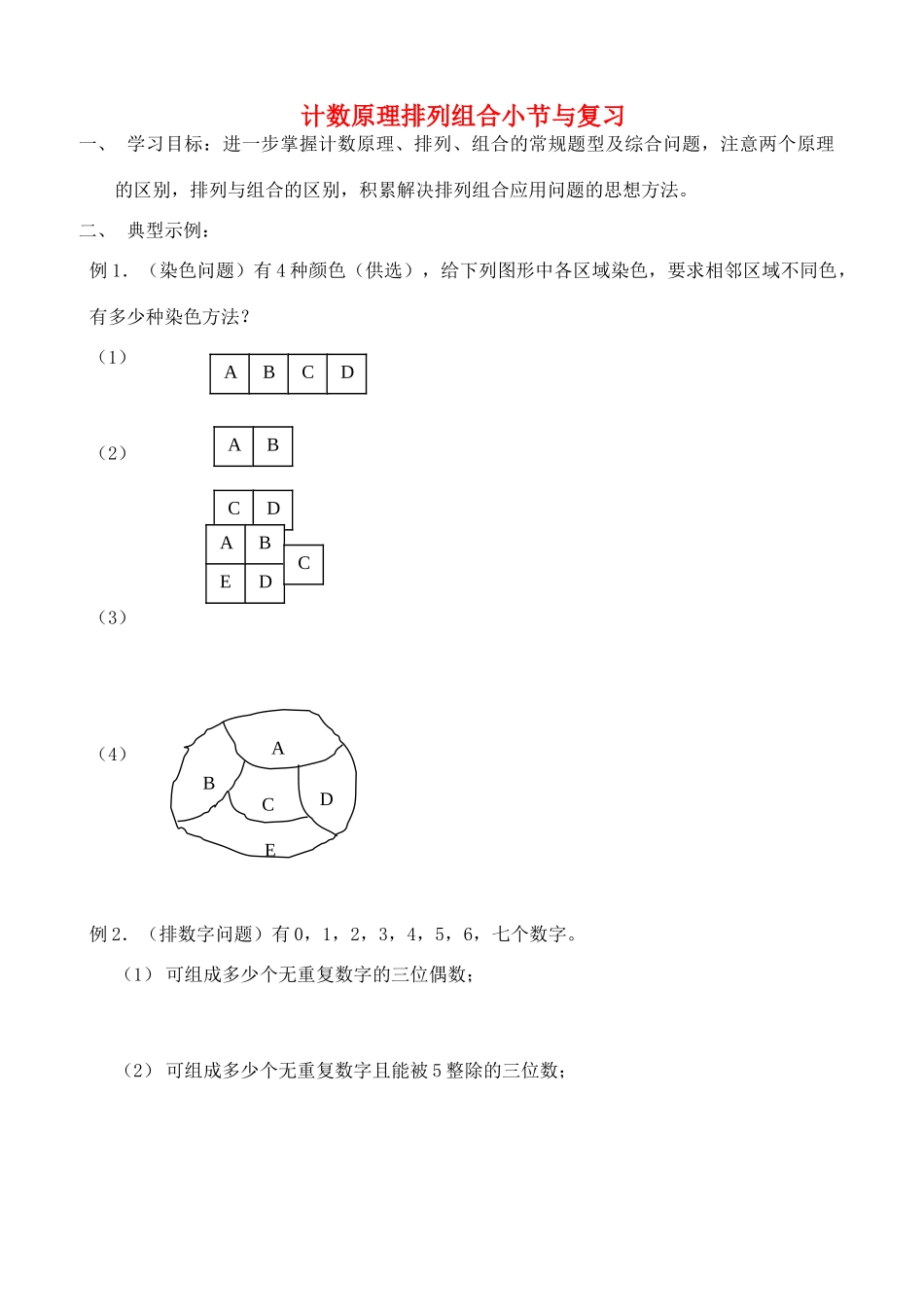
计数原理排列组合小节与复习一、 学习目标:进一步掌握计数原理、排列、组合的常规题型及综合问题,注意两个原理的区别,排列与组合的区别,积累解决排列组合应用问题的思想方法。二、 典型示例:例 1.(染色问题)有 4 种颜色(供选),给下列图形中各区域染色,要求相邻区域不同色,有多少种染色方法?(1)(2)(3)(4)例 2.(排数字问题)有 0,1,2,3,4,5,6,七个数字。(1) 可组成多少个无重复数字的三位偶数;(2) 可组成多少个无重复数字且能被 5 整除的三位数;ABCDABCDABEDCCABDE(3) 可组成多少个无重复数字且能被 3 整除的三位数;(4) 可组成多少个无重复数字且比 315 小的三位数。例 3.(排队照相问题)解决下列问题,掌握解决问题的方法。(1)7 名学生站成一排照相,其中甲不站左端,乙不站右端,有多少种站法?(2)7 名学生站成一排照相,其中甲、乙相邻且都与丙不相邻,有多少种站法?(3)7 名学生站成一排照相,其中甲、乙在丙的同侧,有多少种站法?(4)7 名学生站成一排照相,7 人身高各不相同,要求中间高两边低,有多少种站法?(5)8 名学生站成两排照相,要求后排 4 人都比前排对应的 4 人高,有多少种站法?例 4.(小球分配问题)解决下列问题,注意它们的区别并掌握解决问题的方法。(1)把 3 个不同的小球放入 4 个不同的盒子中,有多少种不同放法?(2)把 3 个不同的小球放入 4 个不同的盒子中,每个盒子最多放 1 个,有多少种不同放法?(3)把 4 个不同的小球放入 3 个不同的盒子中,有多少种不同放法?(4)把 4 个不同的小球放入 3 个不同的盒子中,每个盒子最少放一个,有多少种不同放法?(5)把 4 个相同的小球放入 3 个不同的盒子中,每个盒子最少放一个,有多少种不同放法?(7 个小球呢?)(6)把 4 个相同的小球放入 3 个不同的盒子中,盒子可空,有多少种不同放法?(7)把 4 个不同的小球放入 3 个相同的盒子中,有多少种不同放法?三、 补充练习:(1) (2013 山东理)用 0,1,…,9 十个数字,可 以组成有重复数字的三位数的个数为( )A. 243B.252C.261D.279(2) (2013 福建理)满足,且关于的方程有实数解的有序数对的个数为( )A.14B.13C.12D.10(3) (2013 四川理)从这五个数中,每次取出两个不同的数分别为,共可得到的不同值的个数是( )A.B.C.D.(4) ( 2013 大纲文)从进入...