四川省南江四中高一数学初高中衔接教材 平行线分线段成比例定理

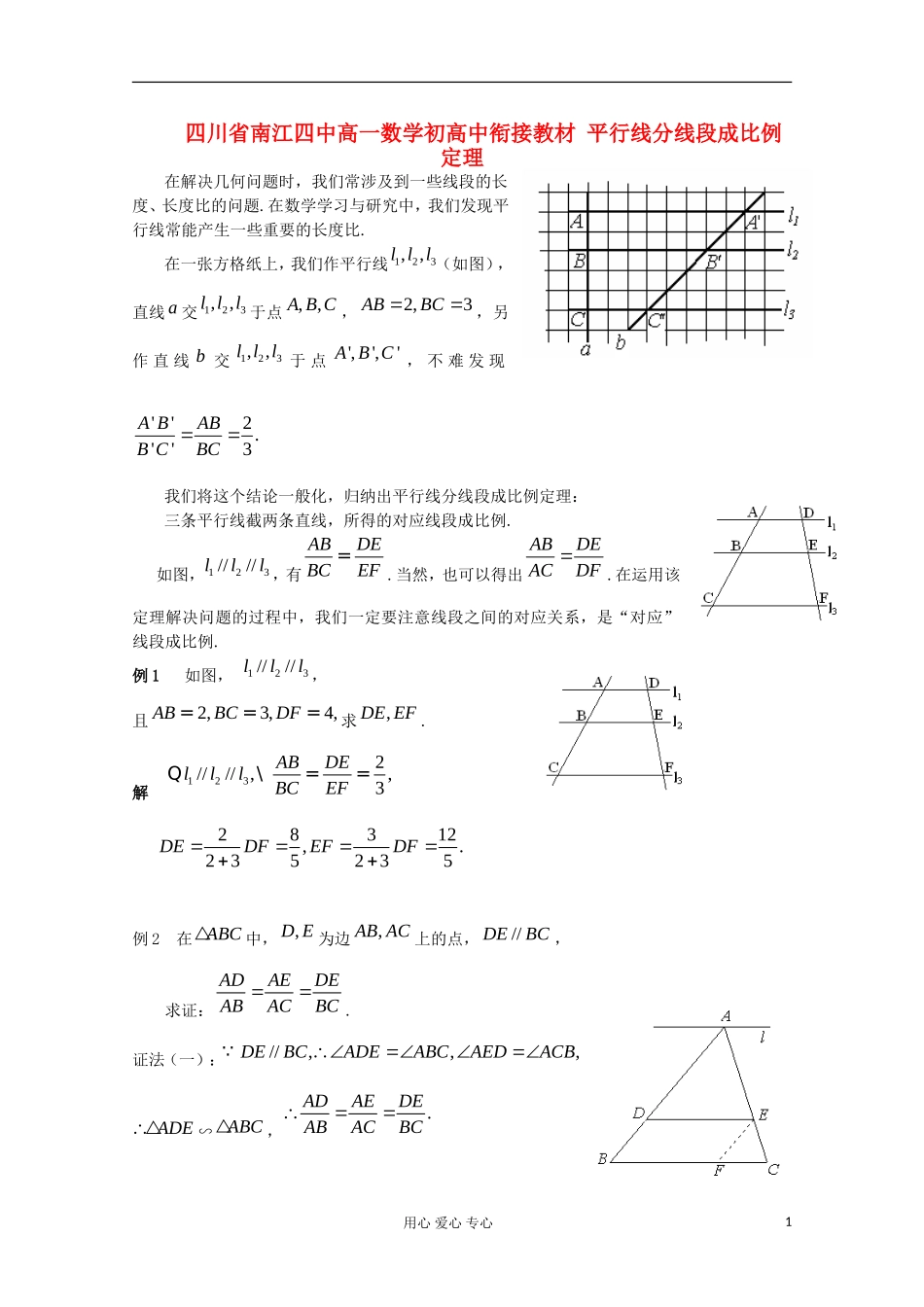
四川省南江四中高一数学初高中衔接教材 平行线分线段成比例定理在解决几何问题时，我们常涉及到一些线段的长度、长度比的问题.在数学学习与研究中，我们发现平行线常能产生一些重要的长度比.在一张方格纸上，我们作平行线 123, ,l l l （如图），直线 a 交 123, ,l l l 于点, ,A B C ，2,3ABBC ，另作 直 线 b 交123, ,l l l 于 点',','A B C ， 不 难 发 现''2.''3A BABB CBC我们将这个结论一般化，归纳出平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例.如图， 123////lll ，有ABDEBCEF=.当然，也可以得出ABDEACDF.在运用该定理解决问题的过程中，我们一定要注意线段之间的对应关系，是“对应”线段成比例.例 1 如图， 123////lll ，且2,3,4,ABBCDF===求,DE EF .解 1232//// ,,3ABDElllBCEF\==Q28312,.235235DEDFEFDF例 2 在 ABC中，,D E 为边,AB AC 上的点，//DEBC ，求证：ADAEDEABACBC.证法（一）：//,,,DEBCADEABCAEDACBADE∽ ABC，.ADAEDEABACBC用心 爱心 专心1证法（二）： 如图 3.1-3，过 A 作直线 //lBC ，////,lDEBCADAEABAC.过 E 作//EFAB 交 AB 于 D ，得BDEF， 因而.DEBF//,.AEBFDEEFABACBCBC .ADAEDEABACBC从上例可以得出如下结论：平行于三角形的一边的直线截其它两边（或两边的延长线），所得的对应线段成比例.平行于三角形的一边，并且和其它两边相交的直线，所截得的三角形的三边与原三角形的三边对应成比例.例 3 已知 ABC，D 在 AC 上，:2:1AD DC ，能否在 AB 上找到一点 E ，使得线段 EC的中点在 BD 上.解 假设能找到，如图，设 EC 交 BD 于 F ，则 F 为 EC 的中点，作//EGAC 交 BD 于G .//,EGAC EFFC， EGFCDF，且 EGDC，1//,2EGADBEGBAD，且1 ,2BEEGBAADE为 AB 的中点.可见，当 E 为 AB 的中点时， EC 的中点在 BD 上.我们在探索一些存在性问题时，常常先假设其存在，再解之，有解则存在，无解或矛盾则不存在.例 4 在ABCV中， AD 为BACÐ的平分线，求证： 用心 爱心 专心2ABBDACDC=.证明 过 C 作 CE//AD，交 BA 延长线于 E，//,.BABDADCEAEDC\=QQAD 平分,,BACBADDACÐ\ Ð=Ð由//ADCE 知,,BADEDACACEÐ=ÐÐ=Ð,,EACEAEAC\ Ð =Ð=即AB...