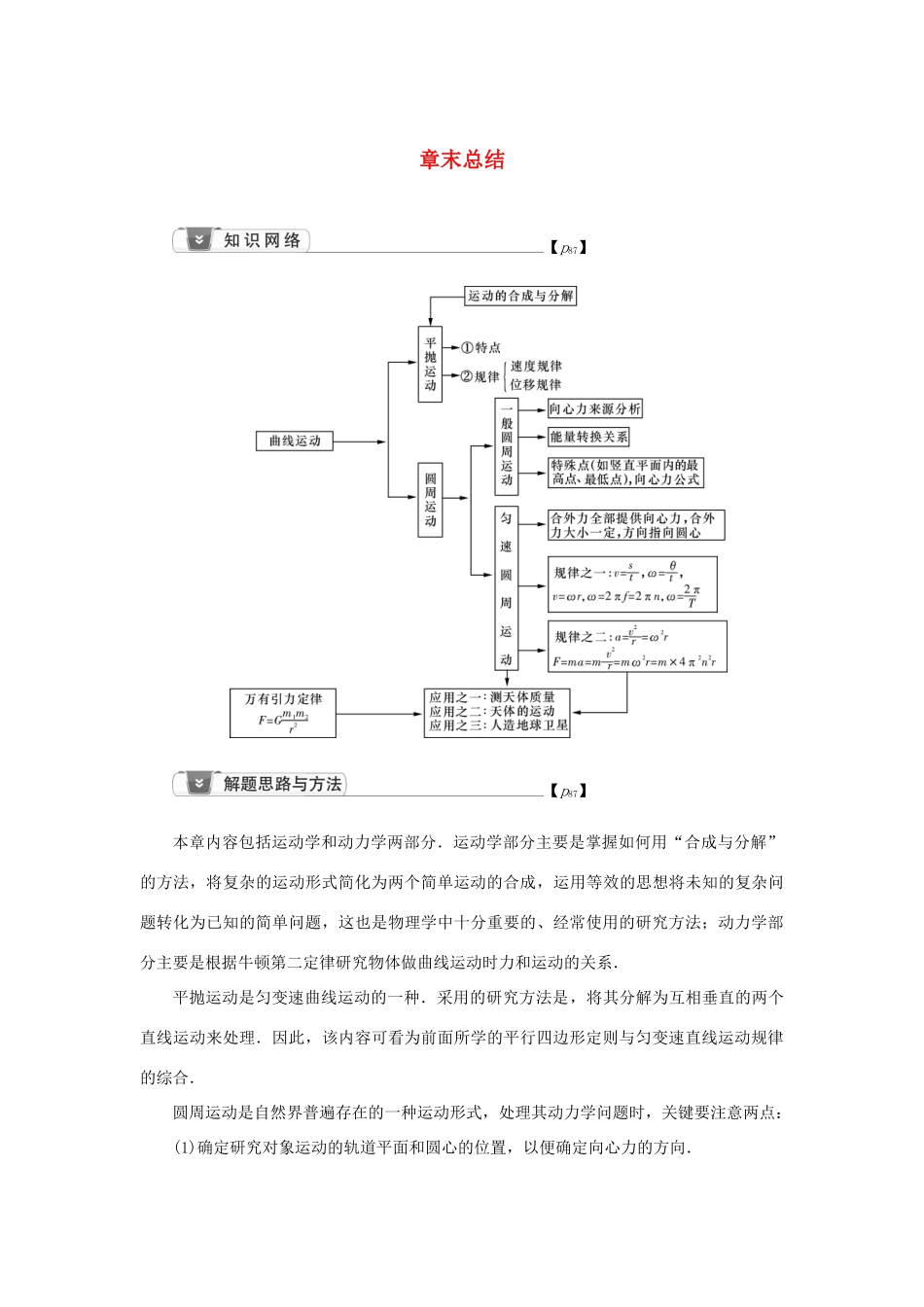
章末总结【p87】【p87】本章内容包括运动学和动力学两部分.运动学部分主要是掌握如何用“合成与分解”的方法,将复杂的运动形式简化为两个简单运动的合成,运用等效的思想将未知的复杂问题转化为已知的简单问题,这也是物理学中十分重要的、经常使用的研究方法;动力学部分主要是根据牛顿第二定律研究物体做曲线运动时力和运动的关系.平抛运动是匀变速曲线运动的一种.采用的研究方法是,将其分解为互相垂直的两个直线运动来处理.因此,该内容可看为前面所学的平行四边形定则与匀变速直线运动规律的综合.圆周运动是自然界普遍存在的一种运动形式,处理其动力学问题时,关键要注意两点:(1)确定研究对象运动的轨道平面和圆心的位置,以便确定向心力的方向.(2)向心力不是和重力、弹力、摩擦力相并列的性质力,它是根据力的作用效果命名的.切不可在物体间的相互作用力以外再添加一个向心力.研究竖直平面内的圆周运动要抓住各种约束物的区别以及运动物体在最高点、最低点的受力特征,并结合牛顿第二定律求解.牛顿运动定律在卫星与天体运动中的应用,不可避免地要密切结合万有引力定律.这类问题需把握以下几个重要方面:①运动模型的建立:A 星绕 B 星做匀速圆周运动;②由 A星与 B 星之间的万有引力提供 A 星运动所需的向心力;③合理选择向心力的表达式,列出万有引力等于向心力的方程,推导出线速度、角速度、周期、半径、向心加速度、中心天体 B 的质量等等的表达式;④重力加速度 g 这一概念的迁移:星球表面有 GM=gR2,这一式子又称“黄金代换式”,不仅可用于地球表面,也可用于其他星球表面;⑤地球表面卫星高空卫星、极地卫星、赤道卫星、同步卫星、三个宇宙速度等的含义要深刻领会、准确掌握,才能在处理问题时应用自如.【p87】1.(多选)(2019·全国卷Ⅱ)如图(a),在跳台滑雪比赛中,运动员在空中滑翔时身体的姿态会影响其下落的速度和滑翔的距离.某运动员先后两次从同一跳台起跳,每次都从离开跳台开始计时,用 v 表示他在竖直方向的速度,其 v-t 图象如图(b)所示,t1和 t2是他落在倾斜雪道上的时刻.则( )A.第二次滑翔过程中在竖直方向上的位移比第一次的小B.第二次滑翔过程中在水平方向上的位移比第一次的大C.第二次滑翔过程中在竖直方向上的平均加速度比第一次的大D.竖直方向速度大小为 v1时,第二次滑翔在竖直方向上所受阻力比第一次的大[解析] 由 v-t 图面积易知第二次面积大于等于第一次面积...