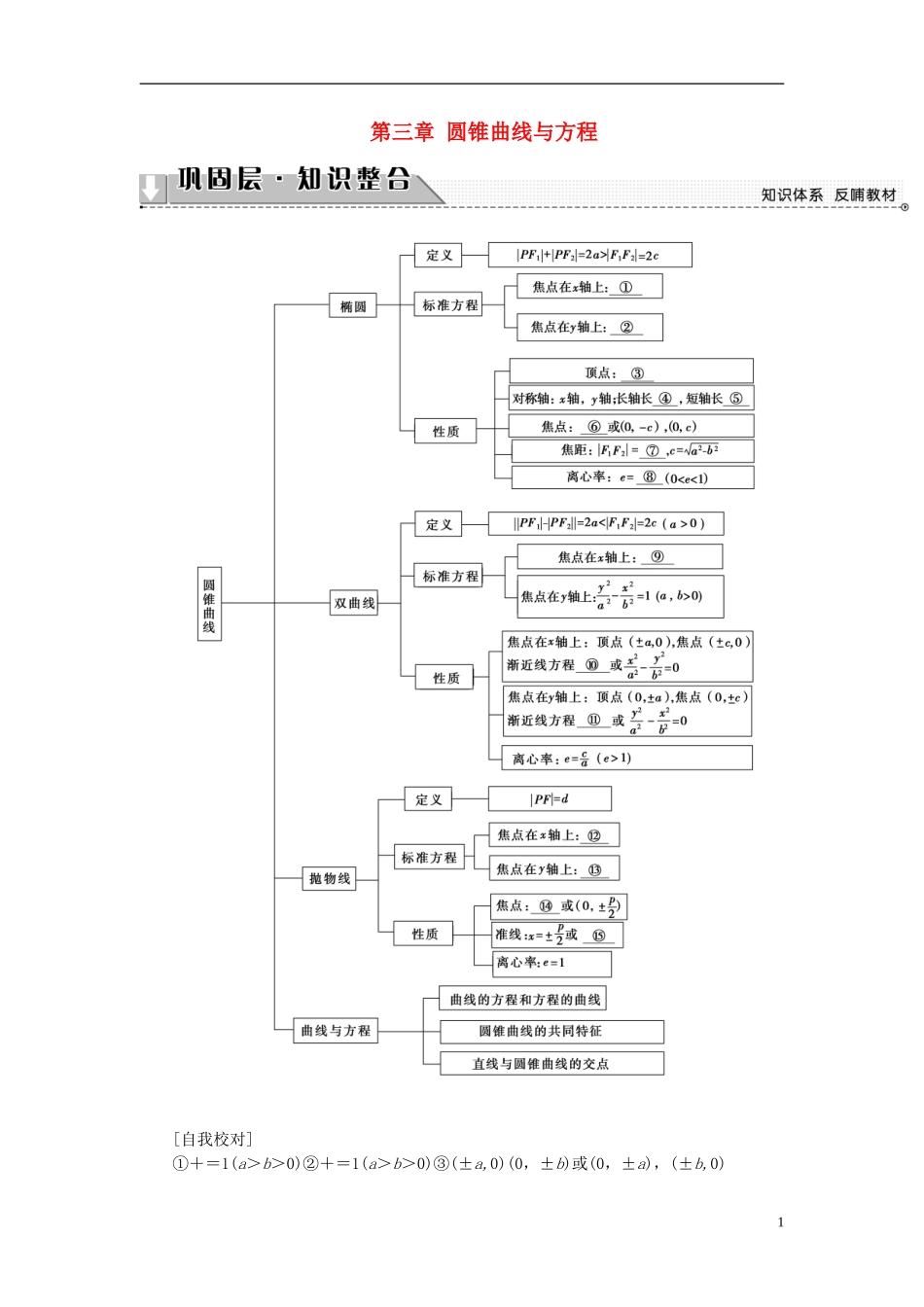
第三章 圆锥曲线与方程[自我校对]①+=1(a>b>0)②+=1(a>b>0)③(±a,0)(0,±b)或(0,±a),(±b,0)1④2a⑤2b⑥(-c,0),(c,0)⑦2c⑧⑨-=1(a,b>0)⑩y=±x⑪y=±x⑫y2=±2px(p>0)⑬x2=±2py(p>0)⑭⑮y=±圆锥曲线的定义及应用圆锥曲线的定义是相应标准方程和几何性质的“源”,对于圆锥曲线的有关问题,要有运用圆锥曲线定义解题的意识,“回归定义”是一种重要的解题策略.如:(1)在求轨迹时,若所求轨迹符合某种圆锥曲线的定义,则根据圆锥曲线的方程,写出所求的轨迹方程;(2)涉及椭圆、双曲线上的点与两个焦点构成的三角形问题时,常用定义结合解三角形的知识来解决;(3)在求有关抛物线的最值问题时,常利用定义把到焦点的距离转化为到准线的距离,结合几何图形利用几何意义去解决. 设 F1、F2是椭圆+=1 的两个焦点,P 为椭圆上的一点,已知 P、F1、F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,求的值.【精彩点拨】 要求的值,可考虑利用椭圆的定义和△PF1F2为直角三角形的条件,求出|PF1|和|PF2|的值,但 Rt△PF1F2的直角顶点不确定,故需要分类讨论.【自主解答】 由题意知,a=3,b=2,则 c2=a2-b2=5,即 c=,由椭圆定义知|PF1|+|PF2|=6,|F1F2|=2.(1)若∠PF2F1为直角,则|PF1|2=|F1F2|2+|PF2|2,|PF1|2-|PF2|2=20,即,解得|PF1|=,|PF2|=.所以=.(2)若∠F1PF2为直角,则|F1F2|2=|PF1|2+|PF2|2.即 20=|PF1|2+(6-|PF1|)2,解得|PF1|=4,|PF2|=2 或|PF1|=2,|PF2|=4(舍去.)所以=2.[再练一题]1.已知点 M(-3,0)、N(3,0)、B(1,0),动圆 C 与直线 MN 切于点 B,过点 M、N 与圆 C 相切的两直线相交于点 P,则 P 点的轨迹方程为( )A.x2-=1(x>1) B.x2-=1(x<-1)C.x2+=1(x>0)D.x2-=1(x>1)【解析】 设 PM、PN 与⊙C 分别切于点 E、F,如图,则|PE|=|PF|,|ME|=|MB|,|NF|=|NB|.从而|PM|-|PN|=|ME|-|NF|=|MB|-|NB|=4-2=2<|MN|,∴P 点的轨迹是以 M、N 为焦点,实轴长为 2 的双曲线的右支(除去右顶点).∴所求轨迹方程为 x2-=1(x>1).2【答案】 A圆锥曲线简单性质的应用有关圆锥曲线的焦点、离心率、渐近线等问题是考试中常见的问题,只要掌握基本公式和概念,并且充分理解题意,大都可以顺利求解. 已知椭圆+=1(a>b>0)的左焦点为 F1(-c,0),A(-a,0),B(0,b)是两个顶点,如果 F1到直线 AB 的距离为,求椭圆的离...