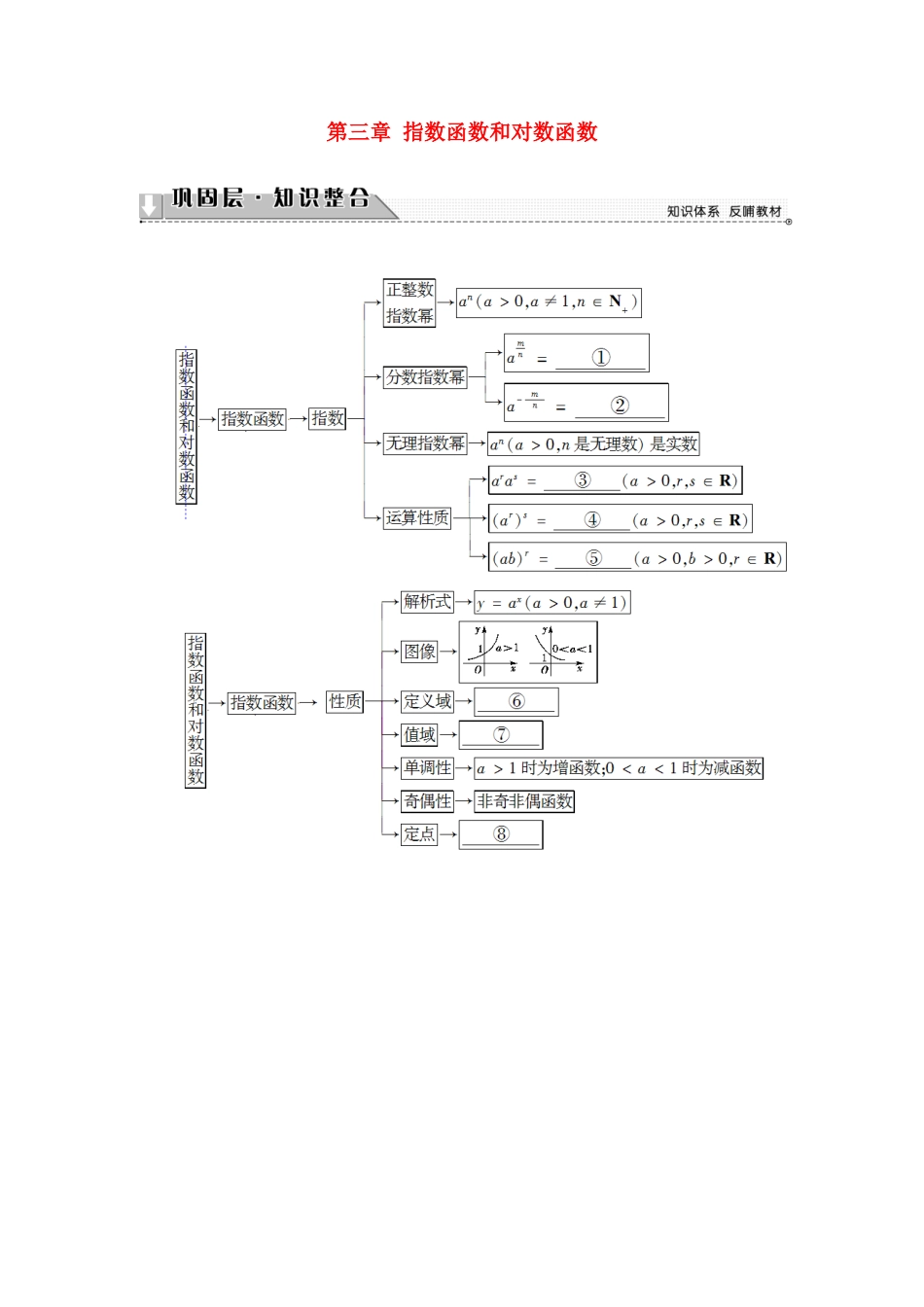
第三章 指数函数和对数函数[自我校对]①② ③ar+s④ars⑤arbr⑥R⑦(0,+∞)⑧(0,1)⑨0⑩1⑪logaM+logaN⑫logaM-logaN⑬nlogaM 指数、对数函数的运算 1. 指数与指数运算、对数与对数运算是两个重要的知识点,不仅是本章考查的重要问题类型,也是高考的必考内容. 2. 指数式的运算首先要注意化简顺序,一般将负指数先转化成正指数、根式化为指数运算,其次若出现分式则要注意对分子、分母进行因式分解以达到约分的目的.对数运算首先注意公式应用过程中范围的变化,前后要等价.运用对数的三个运算性质并结合对数恒等式、换底公式是对数计算、化简、证明常用的技巧. 计算:(1)lg 52+lg 8+lg 5lg 20+(lg 2)2;(2) .【精彩点拨】 利用对数的运算法则,指数的运算法则化简求值.【规范解答】 (1)原式=2lg 5+2lg 2+lg 5(1+lg 2)+(lg 2)2=2(lg 2+lg 5)+lg 5+lg 2×lg 5+(lg 2)2=2+lg 5+lg 2(lg 5+lg 2)=2+lg 5+lg 2=3.[再练一题] 1. (2016·浙江高考) 已知 a>b>1,若 logab+logba=,ab=ba,则 a=________,b=________.【解析】 logab+logba=logab+=,∴logab=2 或. a>b>1,∴logab0,且 a≠1),对数函数 y=logax(a>0,且 a≠1)的图像与性质都与 a 的取值有密切的关系,a 变化时,函数的图像与性质也随之改变.因此,在求解问题时,当 a 的值不确定时,要对它进行分类讨论. 已知函数 f(x)是定义在 R 上的偶函数,当 x≥0 时,f(x)=x.图 31(1)画出函数 f(x)的图像;(2)根据图像写出 f(x)的单调区间,并写出函数的值域.【精彩点拨】 利用偶函数图像关于 y 轴对称,作出函数 f(x)的图像.【规范解答】 (1)先作出当 x≥0 时,f(x)=x的图像,利用偶函数的图像关于 y 轴对称,再作出 f(x)在 x∈(-∞,0)时的图像.(2)函数 f(x)的单调递增区间为(-∞,0),单调递减区间为[0,+∞),值域为(0,1].[再练一题] 2. 当 0