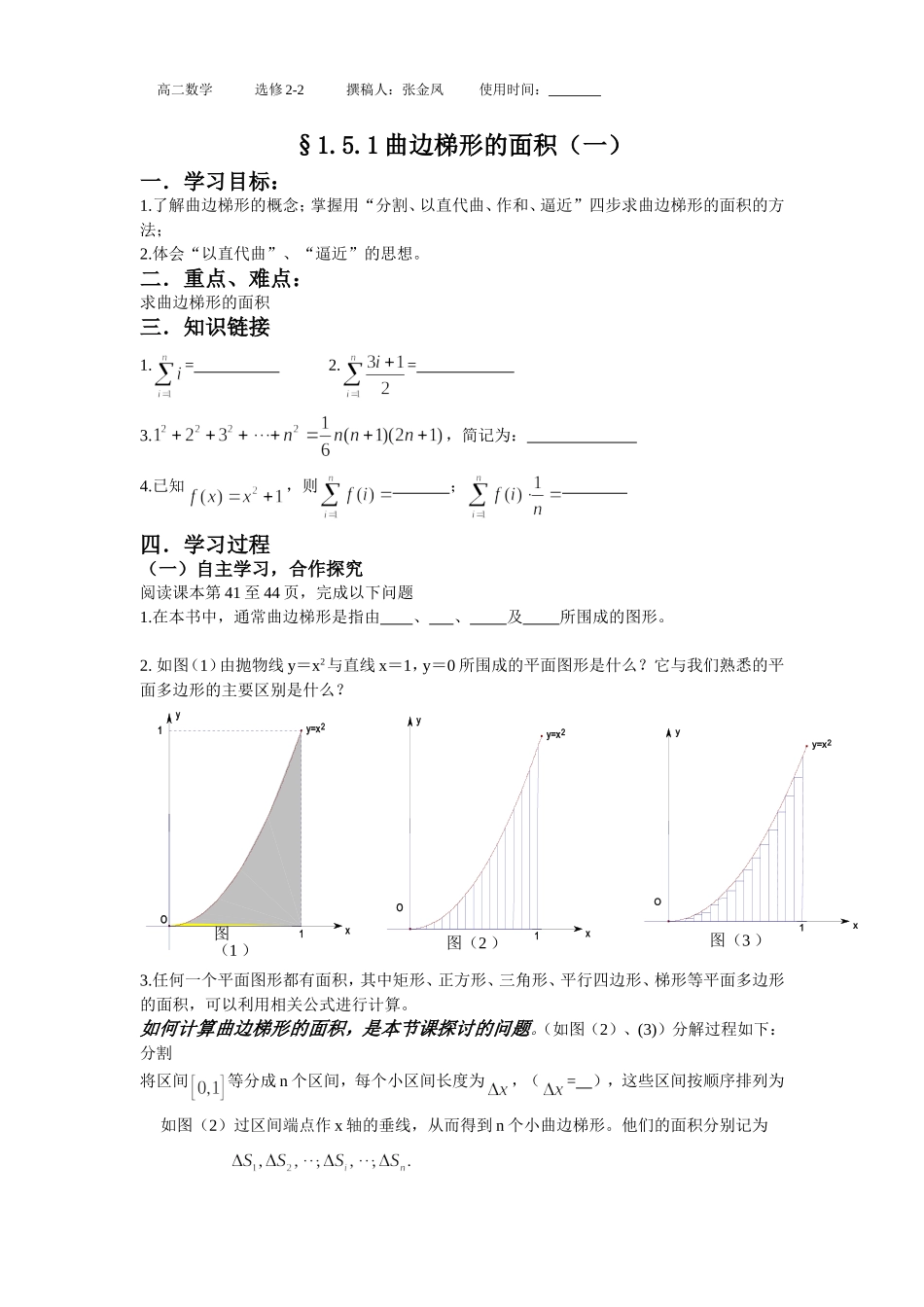
§1.5.1 曲边梯形的面积(一)一.学习目标:1.了解曲边梯形的概念;掌握用“分割、以直代曲、作和、逼近”四步求曲边梯形的面积的方法;2.体会“以直代曲”、“逼近”的思想。二.重点、难点:求曲边梯形的面积三.知识链接1.= 2.= 3.,简记为: 4.已知,则 ; 四.学习过程 (一)自主学习,合作探究阅读课本第 41 至 44 页,完成以下问题1.在本书中,通常曲边梯形是指由 、 、 及 所围成的图形。2. 如图(1)由抛物线 y=x2与直线 x=1,y=0 所围成的平面图形是什么?它与我们熟悉的平面多边形的主要区别是什么?3.任何一个平面图形都有面积,其中矩形、正方形、三角形、平行四边形、梯形等平面多边形的面积,可以利用相关公式进行计算。如何计算曲边梯形的面积,是本节课探讨的问题。(如图(2)、(3))分解过程如下:分割将区间等分成 n 个区间,每个小区间长度为,(= ),这些区间按顺序排列为 如图(2)过区间端点作 x 轴的垂线,从而得到 n 个小曲边梯形。他们的面积分别记为 11Oy=x2yx图(1 )xyy=x2O1图(3 )1Oy=x2yx图(2 )高二数学 选修 2-2 撰稿人:张金凤 使用时间: 以直代曲对区间上的小曲边梯形,用如图(3)的相应小矩形近似代替,则矩形的长为 ,宽为 ,矩形的面积为 ,从而 作和因为每个小矩形的面积是相应的小曲边梯形面积的 值,所以 n 个小矩形的面积之和 ,就是所求曲边梯形的面积 S= 的近似值 (用符号填写 2、3 两空),即 S= = = = 逼近当分割无限变细,即(亦即)时, 而当时,= (注意:利用链接 3 的公式化简,可参考第 43 页的方法 2) .由此可知曲边梯形的面积 S= .4. 上述用逼近思想求曲边梯形面积的过程有哪几个基本步骤? 5.分割越 ,面积的近似值就越 。当分割无限变细时,这个近似值就无限 所求曲边梯形的面积 S。(二)新知应用,技能培养例 1.计算由抛物线,两直线,及轴所围成的曲边梯形的面积。例 2.用“分割、以直代曲、求和、逼近”,求由所围成的图形的面积。五.基础达标1.(A 级)把区间(1,3)n 等分,所得 n 个小区间每个区间的长度应为 ;2.(A 级)关于近似替代下列说法正确的是( )A.在分割后的每个小区间上,只能用左端点的函数值近似替代;B.在分割后的每个小区间上,只能用右端点的函数值近似替代;C.在分割后的每个小区间上,只能用中间端点的函数值近似替代;D.在分割后的每个小区间上,可以用区间...