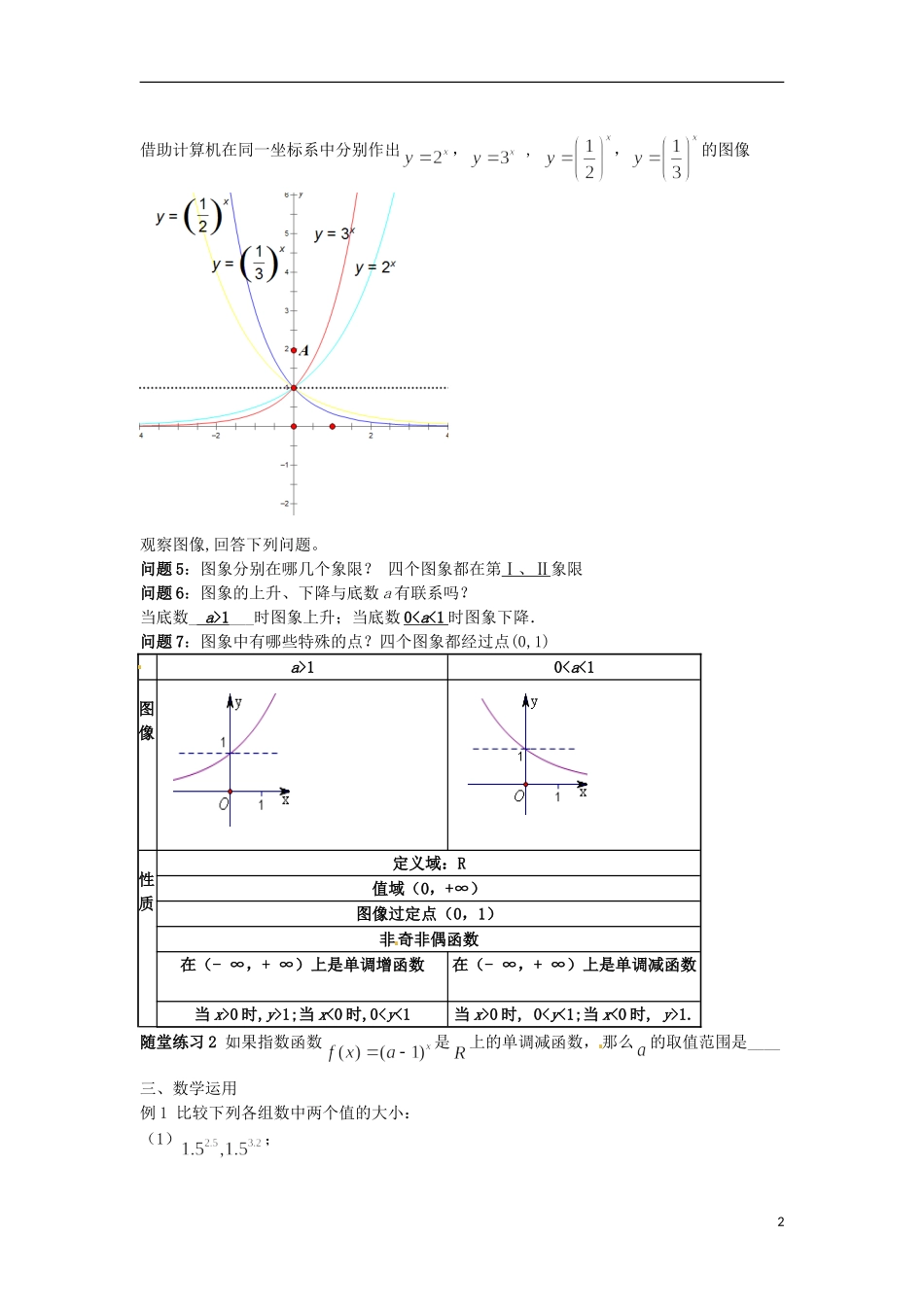
江苏省江阴市成化高级中学 2014 年高中数学 2.1 指数函数教案 新人教版必修 1一. 教学目标:1.知识与技能① 通过实际问题了解指数函数的实际背景;② 理解指数函数的概念和意义,根据图象理解和掌握指数函数的性质.③ 体会具体到一般数学讨论方式及数形结合的思想;2.情感、态度、价值观① 让学生了解数学来自生活,数学又服务于生活的哲理.② 培养学生观察问题,分析问题的能力.3.过程与方法展示函数图象,让学生通过观察,进而研究指数函数的性质.教学过程:一、问题情境:问题 1: 不借助计算器比较两个值的大小:联想到可以利用函数单调性比较大小,为此我们构造函数问题 2:该函数单调性如何呢?二、建构数学:一般地,函数叫做指数函数,它的定义域是 R.问题 3:为什么要规定?若不一定有意义.如时, 取。若,则当时,; 时,无意义。若,则对于任意为常量,无研究价值。为了方便研究,规定:随堂练习 1(1)课本 P67 练习 1在函数①②③④⑤⑥中,哪些是指数函数? (2)函数是指数函数,求的值。问题 4: 我们从哪几个方面研究函数呢?定义域 , 值域 , 单调性 , 奇偶性如果我们知道了一个函数的图像能否看出它的定义域?值域?单调性?奇偶性?1借助计算机在同一坐标系中分别作出, , ,的图像观察图像,回答下列问题。问题 5:图象分别在哪几个象限? 四个图象都在第Ⅰ、Ⅱ象限问题 6:图象的上升、下降与底数 a 有联系吗?当底数_ a >1 ___时图象上升;当底数 0< a <1 时图象下降.问题 7:图象中有哪些特殊的点?四个图象都经过点(0,1) a>10
0 时,y>1;当 x<0 时,00 时, 01.随堂练习 2 如果指数函数是上的单调减函数,那么的取值范围是____三、数学运用例 1 比较下列各组数中两个值的大小:(1);2(2);(3)引导学生思考解决问题的的方法:(1)对于前 2 个问题,底数相同而底数不同,考虑构造 1 个指数函数,利用指数函数单调性来研究。(2)对于第三个问题,底数不同,指数也不同,但根据指数函数性质可以判断其中一个比 1 大,另一个比 1 小,可以找“桥梁 1”来过渡。随堂练习 3 课本 P67 练习 4比较下列各组数中两个值的大小关系:(1) ;(2)(3); (4)(5); (6)例 2(1)已知...