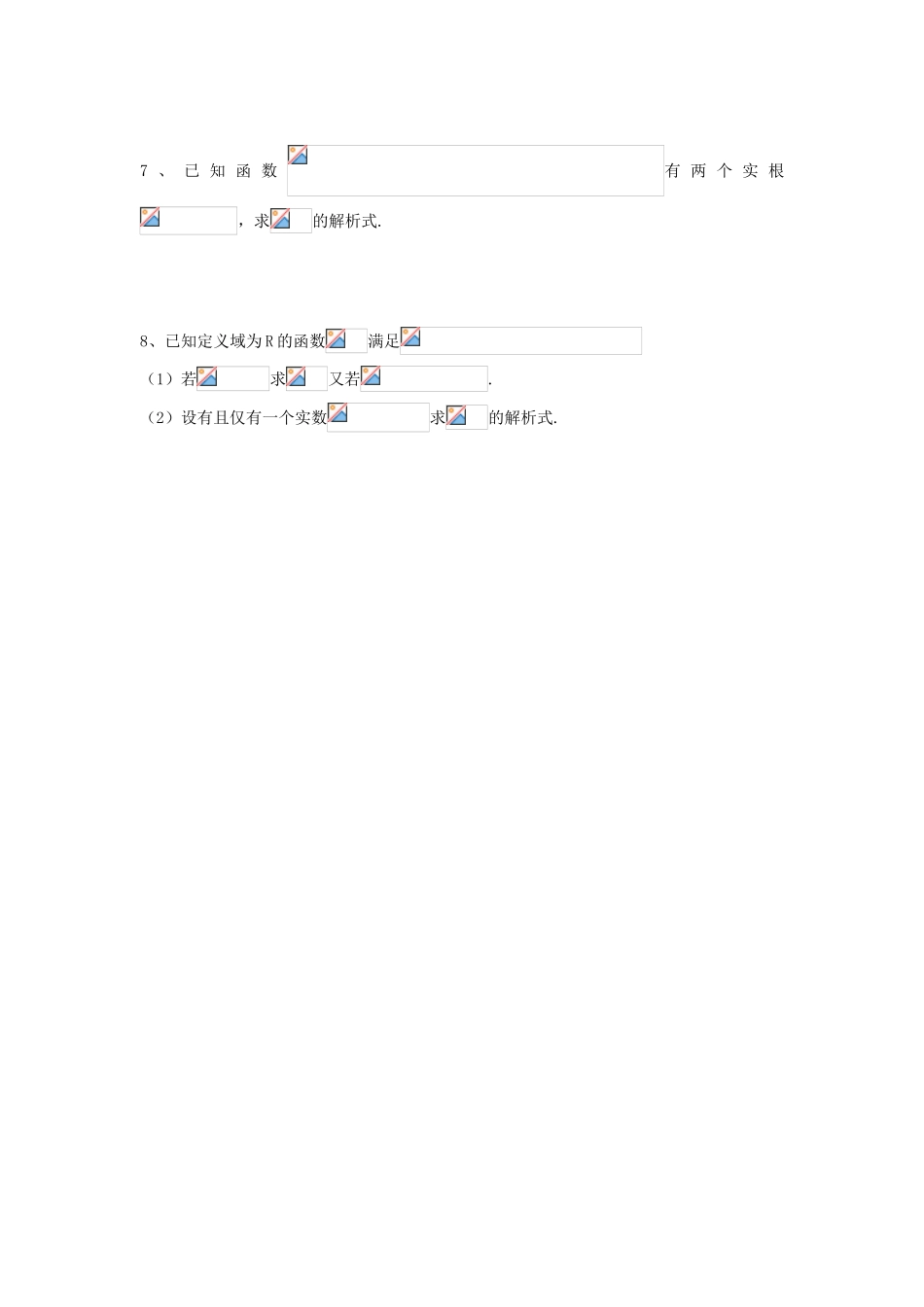
高三数学理科复习 3----函数解析式【高考要求】:函数的有关概念(B).【教学目标】:1.理解函数的三种表示方法(图象法、列表法、解析法),会选择恰当的方法表示简单情境中的函数.2.了解简单的分段函数;能写出简单情境中的分段函数,并能求出给定自变量所对应的函数值,会画函数的图象(不要求根据函数值求自变量的范围).【教学重难点】: 求函数解析式的方法.【知识复习与自学质疑】1 、 已 知则 ____. ._____. .= .2、设则的表达式为 . 3、函数,则 . 4、若,则 . 5、设,则 . 6 、 对记, 则的 最 小 值 为 . 【交流展示与互动探究】1、已知,求的解析式.2、设二次函数的最小值为 4,且求的解析式.3、如图,是边长为 2 的正三角形,设直线截这个三角形所得到的位于此直线上方的图形(阴影部分)的面积为,求的解析式.【矫正反馈】1、若则 . .2、已知则的解析式为 . 3、设函数的图像与的图像关于轴对称,则= .4、一次函数在上的最小值为 1,最大值为 3,则的解析式为 . 5、设,则的解析式为 . 【迁移应用】6、某超市经销某种牙膏,其年销售额为 6000 盒,每盒进价 2.8 元,销售价 3.4 元,全年分若干次进货,每次进货均为盒,已知每次运输劳务费 62.5 元,全年的保管费元(1)把该超市经销牙膏一年的利润元表示为每次进货是的函数.(2)为使利润最大,每次应进多少盒?7 、 已 知 函 数有 两 个 实 根,求的解析式.8、已知定义域为 R 的函数满足(1)若求又若.(2)设有且仅有一个实数求的解析式.