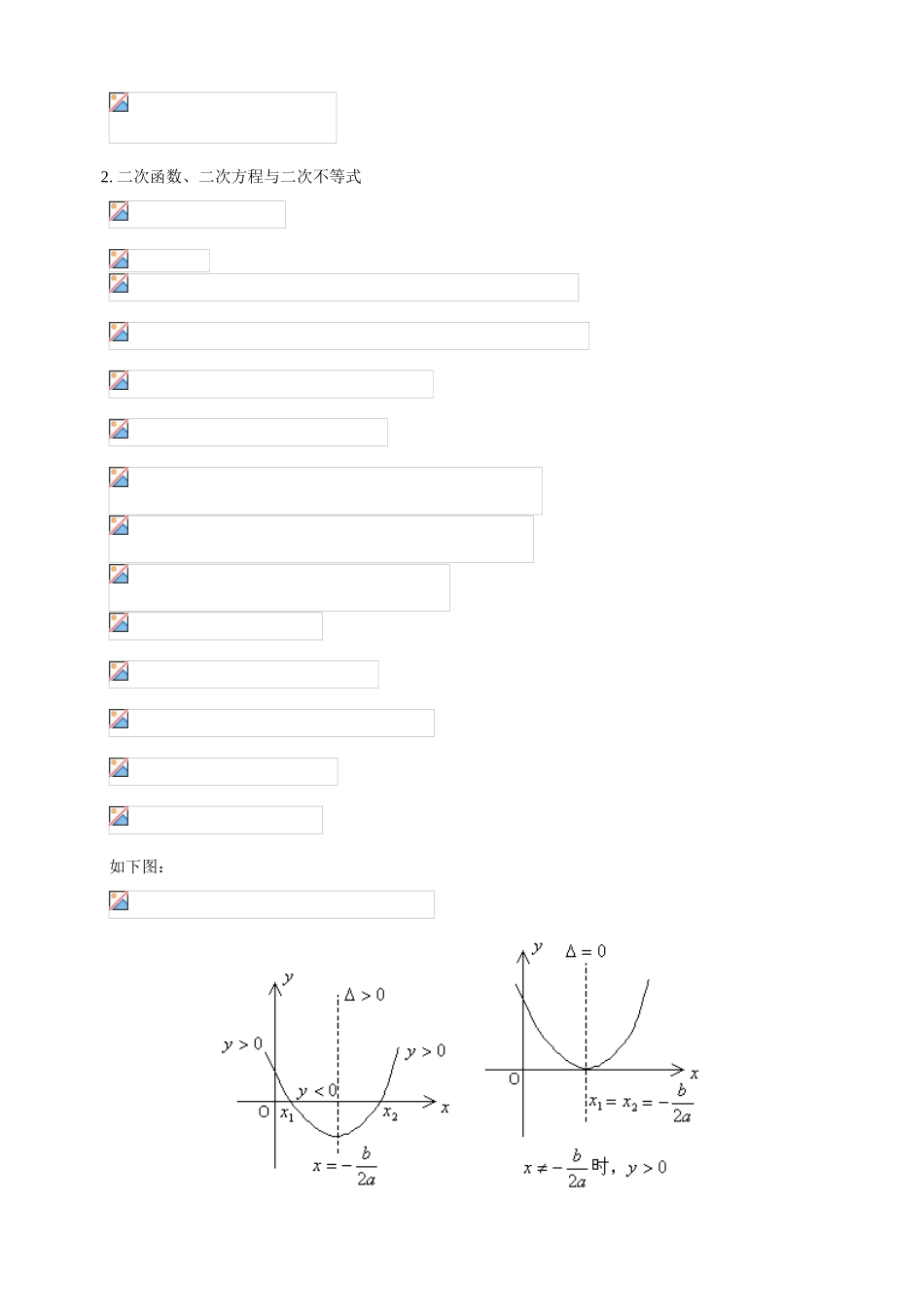
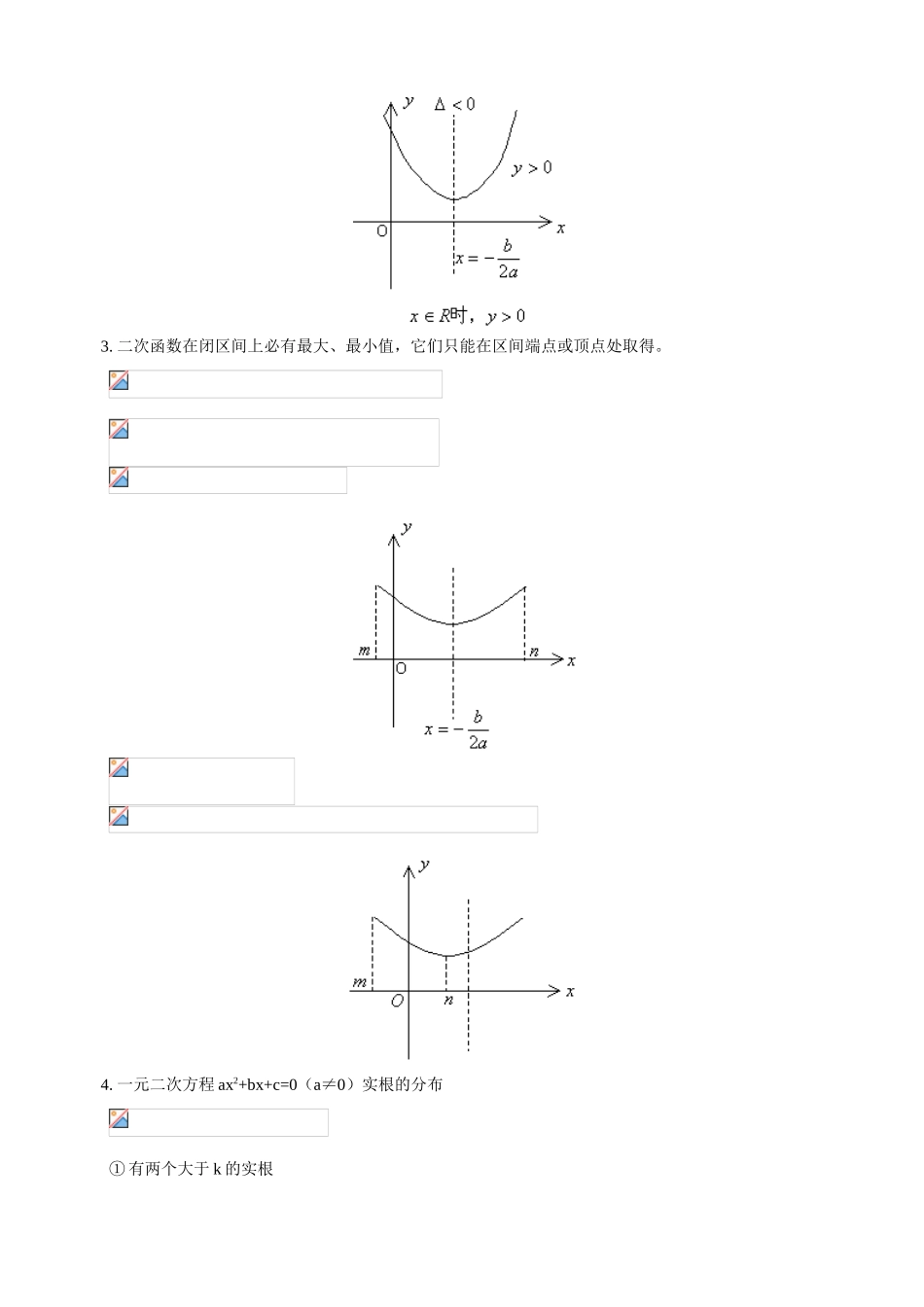
2.4.1 二次函数的图像一. 教学内容: 二次函数的图像二. 教学要求: 1. 掌握二次函数的对称性、单调性、最值公式及图象。理解并掌握二次函数、二次方程与二次 不等式的内在联系,能利用“数形结合”,“判别式”和“韦达定理”讨论二次方程根的情况及二次不等式的解集。 2. 理解分数指数的概念,掌握有理指数幂的运算性质;理解对数的概念,掌握对数的运算性质。 3. 掌握指数与对数函数的概念,图象和性质,会用定义法证明指数函数与对数函数的单调性,能应用其性质解(证)相关问题。三. 知识串讲(一)二次函数 1. 形如 f(x)=ax2+bx+c(a≠0)的函数叫做二次函数。 (1)二次函数的解析式 (2)图象和性质 2. 二次函数、二次方程与二次不等式 如下图: 3. 二次函数在闭区间上必有最大、最小值,它们只能在区间端点或顶点处取得。 4. 一元二次方程 ax2+bx+c=0(a≠0)实根的分布 ① 有两个大于 k 的实根 ② 有两个小于 k 的实根 ③ 有一根大于 k,一根小于 k ④ 两根都在(m,n)内 ⑤ 一根小于 m,一根大于 n ⑥ 两根之一在(m,n)内 ⑦ 一根在(m,n)内,另一根在(n,p)内 注:若不限定 a 的正负时,只要在 f(k)前乘以 a,即 af(k),其余不变。(二)指数与对数函数 1. n 次方根:若 xn=a(n∈N,n>1),则称 x 为 a 的 n 次方程。 性质: 2. 指数 运算法则: 3. 对数 性质: (1)0 和负数没有对数,即 N>0 运算法则:(M>0,N>0) 换底公式: 4. 指数函数与对数函数 图象过点(0,1),以 x 轴 图象过点(1,0),以 y 轴为渐近线为渐近线 底数互为倒数时,图象关于 底数互为倒数时,图象关于 x 轴y 轴对称,x>0 时,“底大图高”对称,x>1 时“底大图低”【典型例题】 例 1. 设二次函数 y=f(x)的最小值等于 4,且 f(0)=f(2)=6,求 f(x)的解析式。 解法一: 解法二: ∴抛物线有对称轴 x=1 又二次函数有最小值 4 代入点(0,6)坐标,得 a=2 例 2. 若方程 x2-11x+(30+a)=0 的两根不等且均大于 5,求实数 a 的取值范围。 解:(法一): (法二): 例 3. 设集合 A={(x,y)|y=x2+ax+2},B={(x,y)|y=x+1,0≤x≤2},A∩B≠φ,求实数 a 的取值范围。 解:(分析:集合的元素是曲线上的点(x,y),A∩B≠φ,即曲线与线段有交点) 点评:对于方程 x2+(a-1)x+1=0 在[0,2]上...