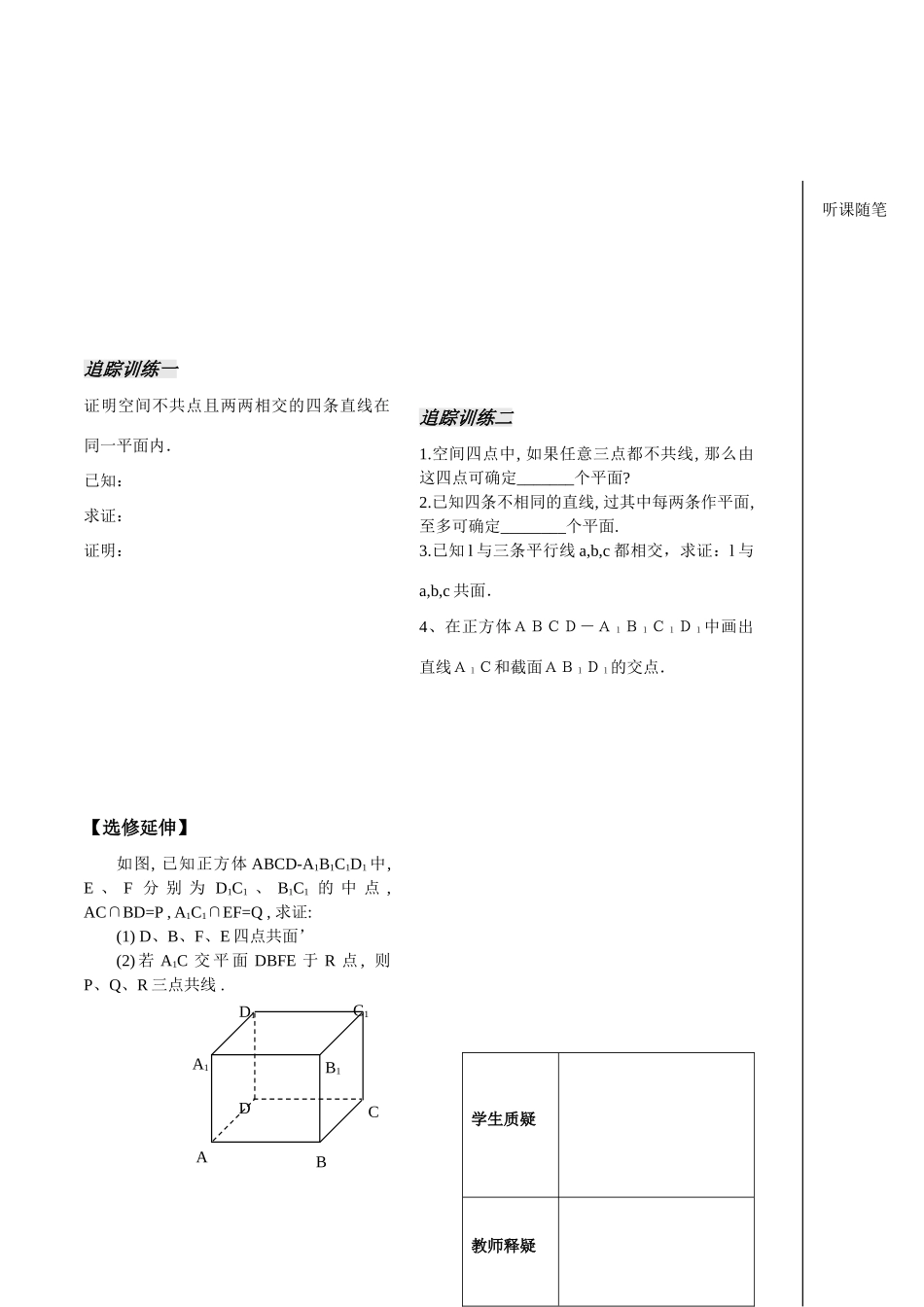
第六课时 平面的基本性质 【学习导航】 知识网络 学习要求 1.了解平面基本性质的 3 个推论, 了解它们各自的作用. 2.能运用平面的基本性质解决一些简单的问题.自学评价1.推论1: . 已知:求证:2.推论2: 已知:求证:3.推论3: 符号表示: 仿推论 1、推论 2 的证明方法进行证明。【精典范例】一、如何证明共面问题.例 1:已知: 如图 A∈l , B∈l, C∈l, Dl, 求证: 直线 AD、BD、CD 共面.思维点拔:简单的点线共面的问题,一般是先由部分点或线确定一个平面,然后证明其他的点线也在这个平面内,这种证明点线共面的方法称为"落入法"例 2.如图: 在长方体 ABCD-A1B1C1D1 中, P为棱 BB1的中点, 画出由 A1 , C1 , P 三点所确定的平面 α 与长方体表面的交线.公理3推论1推论 2推论 3ABDClα听课随笔ABCDD1C1B1A1P追踪训练一证明空间不共点且两两相交的四条直线在同一平面内.已知:求证:证明:【选修延伸】如图, 已知正方体 ABCD-A1B1C1D1 中, E 、 F 分 别 为 D1C1 、 B1C1 的 中 点 , AC∩BD=P , A1C1∩EF=Q , 求证: (1) D、B、F、E 四点共面’(2) 若 A1C 交 平 面 DBFE 于 R 点 , 则P、Q、R 三点共线 .追踪训练二1.空间四点中, 如果任意三点都不共线, 那么由这四点可确定_______个平面?2.已知四条不相同的直线, 过其中每两条作平面, 至多可确定________个平面.3.已知 l 与三条平行线 a,b,c 都相交,求证:l 与a,b,c 共面.4、在正方体ABCD-A1B1C1D1中画出直线A1C和截面AB1D1的交点. 学生质疑教师释疑ABCDD1C1B1A1听课随笔