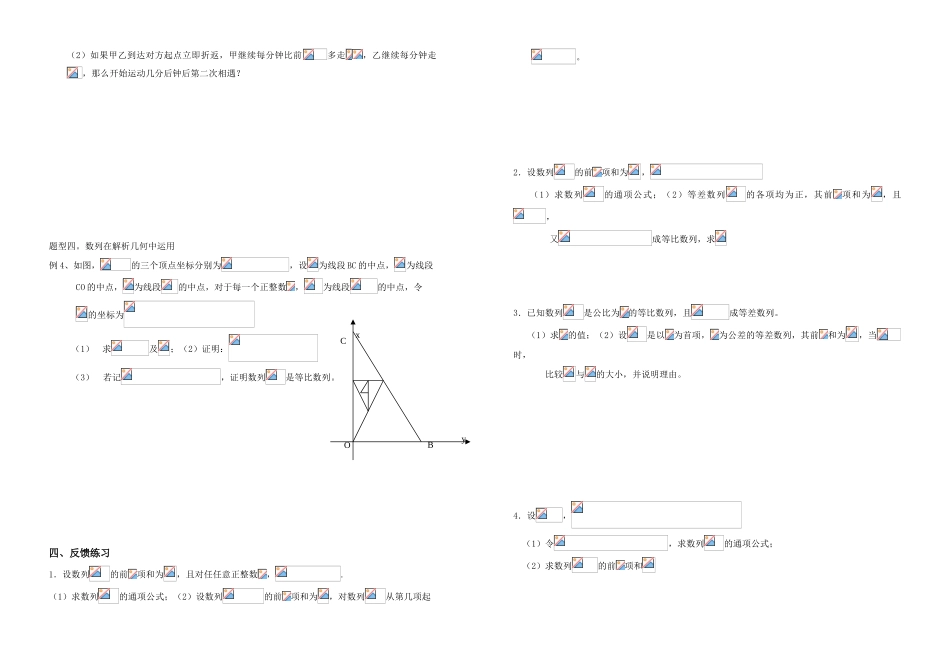
课题：数列的综合运用备课时间:2008 年 9 月 3 日 主备人:周立能 总课时数：015一、知识点梳理1．正确理解数列的前和的概念，掌握一般数列的求和方法和变形技巧2．掌握数列（特别是等差数列，等比数列）的概念，通项公式及前和公式，并能运用这些这知识解决实际应用问题和数列综合问题
3．会用观察、归纳、类比、联想、转化和分类讨论的数学思想求数列的前和，从 而培养学生的化归能力，训练学生思维的灵活性，提高学生综合运用知识能力
4．培养学生的分析理解能力，数学建模能力和综合运算能力，突出数学的发散思维 功能以及解决实际问题的应用技能
二、基础巩固练习1．设，求2．数列的前项和为，关于数列有下列三个命题： （1）若既是等差数列又是等比数列，则 （2）若，则是等差数列； （3）若，则是等比数列
这些命题中，真命题的序号是3．是首项为 的正项数列，且，则它的通项公式4．已知定义为R的函数满足， 若，成等三、例题精选题型一、递推公式的应用例 1、数列满足，且，记（1）求的值
（2）求数列的通项公式及数列的前项和题型二、中项式的应用例 2、（1）设是三个实数，且成等比数列，成等差数列，求（2）在数列中，设，并且连续三项满足：当为奇数时，它们成等比数列；当为偶数时，它们成等数列
现将数列的各奇数项按从小到大的顺序依次取出，作成一个新数列，求新数列的通项公式
题型三、数列的实际应用例 3、甲乙两物体分别从相距 70的两处同时相向运动
甲第走，已后每分钟比前多走，乙每分钟走（1）甲乙开始运动后几分钟相遇
（2）如果甲乙到达对方起点立即折返，甲继续每分钟比前多走，乙继续每分钟走，那么开始运动几分后钟后第二次相遇
数列在解析几何中运用例 4、如图，的三个顶点坐标分别为，设为线段 BC 的中点，为线段 CO 的中点，为线段的中点，对于每一个正整数，为线段的中点，令 的坐标为（1）求及；（2
