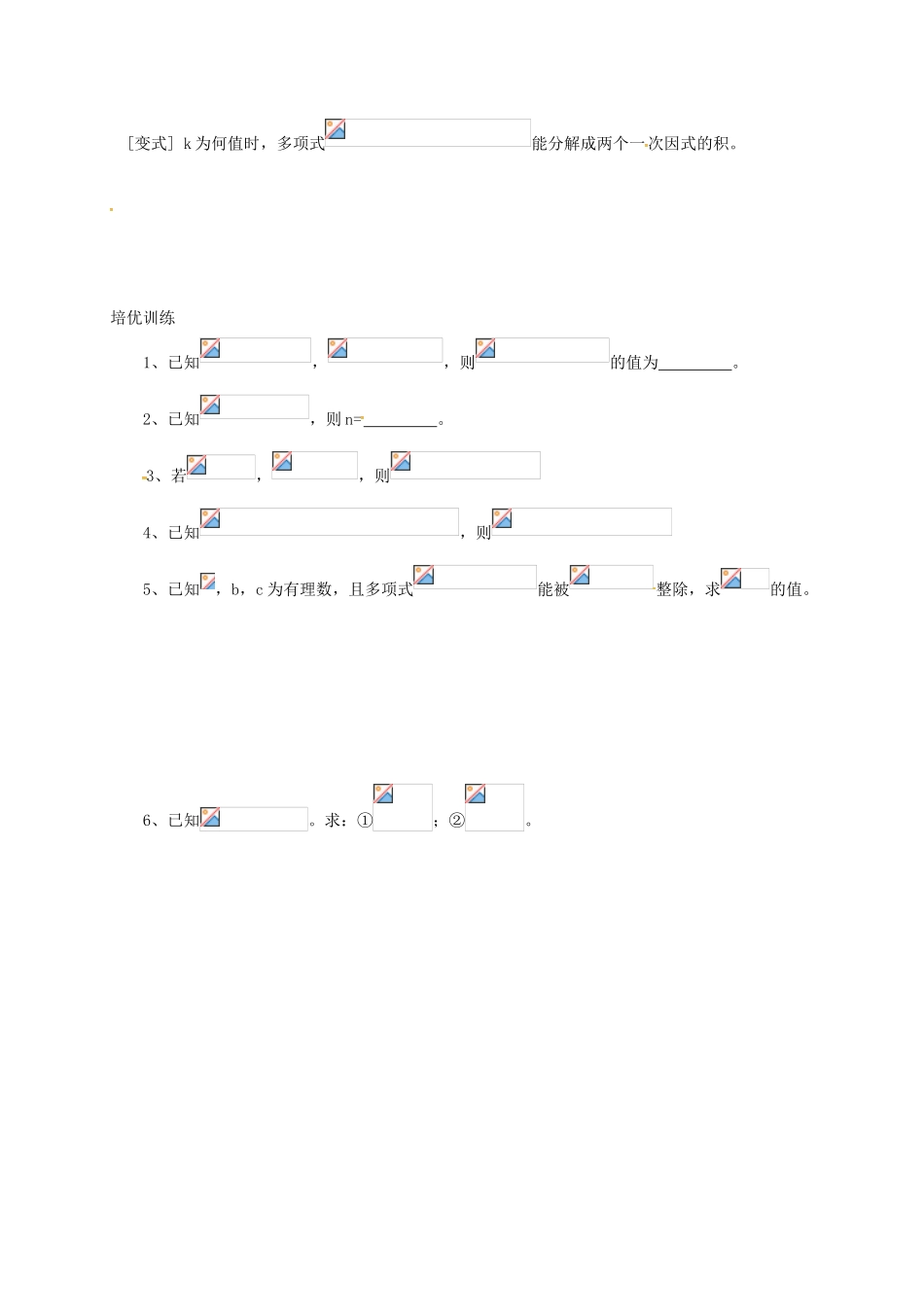
专题四:整式运算技巧典例导析类型一:运用整体思想进行整式运算例 1:假如时,代数式的值为 5,那么时,原代数式的值为 。 [点拨] 找出式中不变的整体。 [解答] [变式] 若,则类型二:活用幂的运算法则例 2:①已知,则 m= 。 ② 已知,则 [点拨] 正用、反用、活用幂的运算法则。 [解答] [变式] 已知,,则类型三:活动乘法公式例 3:已知,,,则多项式的值为 。 [点拨] 运用完全平方将多项式变形 [解答] [变式] 已知,y 满足。求代数式的值。类型四:()的应用例 1:①当时,x 的取值范围为 。 ② 方程的整数解的个数为 。 [点拨] 注意中之隐条件。 [解答] [变式] 若无意义,则代数式类型五:多项式的余数定理例 5:若多项式能被整除,则= ,b= 。 [点拨] 余数定理:若能被整除,则。 [解答] [变式] 若多项式被除后余 3,则 k= 。类型六:巧用因式分解例 6: 已知,b,x,y 满足,, 则。 [点拨] 将式子因式分解。 [解答] [变式] 已知△ABC 中,三边长,b,c 满足等式。 求证:。类型七:用待定系数法分解因式例 7:分解因式 [点拨] 可抓住齐二次项或主元 x 或 y 分解。 [解答] [变式] k 为何值时,多项式能分解成两个一次因式的积。培优训练1、已知,,则的值为 。2、已知,则 n= 。3、若,,则4、已知,则5、已知,b,c 为有理数,且多项式能被整除,求的值。6、已知。求:①;②。7、已知,,且。求的值。竞赛训练1、若实数,b,c,d 满足,则四个数中最大的是 。2、比较,,的大小。3、设,b,c,d 都是正整数,且,,。求 d-b 的值。4、已知,b,c 满足,,则的值是 。5、某校进行春季运动会时,由若干名同学组成一个 8 列的长方形队列。假如原队列中增加 120人,就能组成一个正方形队列;假如原队列中减少 120 人,也能组成一个正方形队列。问原长方形队列有多少名同学?