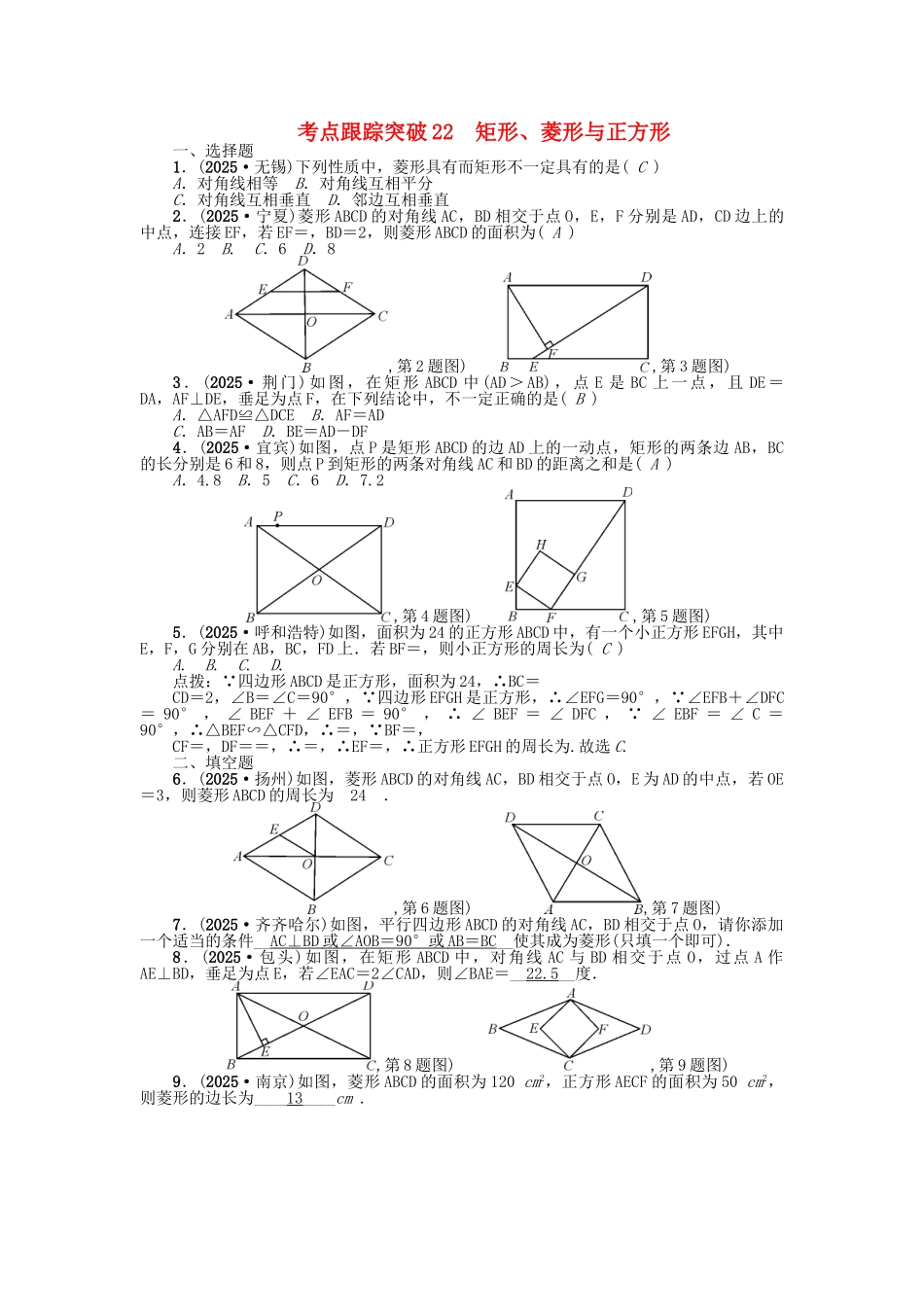
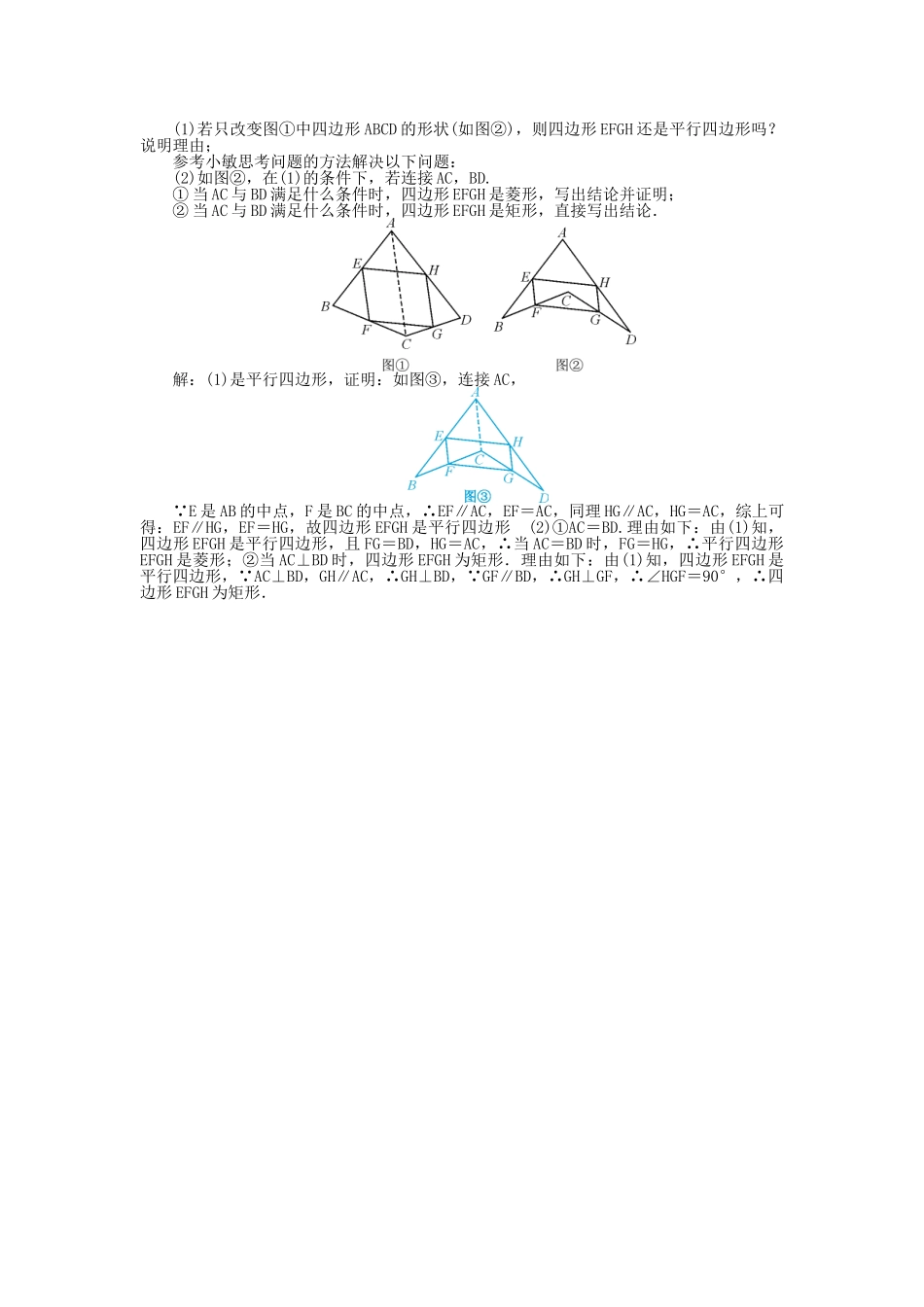
考点跟踪突破 22 矩形、菱形与正方形一、选择题1.(2025·无锡)下列性质中,菱形具有而矩形不一定具有的是( C )A.对角线相等 B.对角线互相平分C.对角线互相垂直 D.邻边互相垂直2.(2025·宁夏)菱形 ABCD 的对角线 AC,BD 相交于点 O,E,F 分别是 AD,CD 边上的中点,连接 EF,若 EF=,BD=2,则菱形 ABCD 的面积为( A )A.2 B. C.6 D.8,第 2 题图) ,第 3 题图)3.(2025·荆门)如图,在矩形 ABCD 中(AD>AB),点 E 是 BC 上一点,且 DE=DA,AF⊥DE,垂足为点 F,在下列结论中,不一定正确的是( B )A.△AFD≌△DCE B.AF=ADC.AB=AF D.BE=AD-DF4.(2025·宜宾)如图,点 P 是矩形 ABCD 的边 AD 上的一动点,矩形的两条边 AB,BC的长分别是 6 和 8,则点 P 到矩形的两条对角线 AC 和 BD 的距离之和是( A )A.4.8 B.5 C.6 D.7.2,第 4 题图) ,第 5 题图)5.(2025·呼和浩特)如图,面积为 24 的正方形 ABCD 中,有一个小正方形 EFGH,其中E,F,G 分别在 AB,BC,FD 上.若 BF=,则小正方形的周长为( C )A. B. C. D.点拨: 四边形 ABCD 是正方形,面积为 24,∴BC=CD=2,∠B=∠C=90°, 四边形 EFGH 是正方形,∴∠EFG=90°, ∠EFB+∠DFC= 90° , ∠ BEF + ∠ EFB = 90° , ∴ ∠ BEF = ∠ DFC , ∠ EBF = ∠ C =90°,∴△BEF∽△CFD,∴=, BF=,CF=,DF==,∴=,∴EF=,∴正方形 EFGH 的周长为.故选 C.二、填空题6.(2025·扬州)如图,菱形 ABCD 的对角线 AC,BD 相交于点 O,E 为 AD 的中点,若 OE=3,则菱形 ABCD 的周长为__24__.,第 6 题图) ,第 7 题图)7.(2025·齐齐哈尔)如图,平行四边形 ABCD 的对角线 AC,BD 相交于点 O,请你添加一个适当的条件__AC⊥BD 或∠ AOB = 90° 或 AB = BC __使其成为菱形(只填一个即可).8.(2025·包头)如图,在矩形 ABCD 中,对角线 AC 与 BD 相交于点 O,过点 A 作AE⊥BD,垂足为点 E,若∠EAC=2∠CAD,则∠BAE=__22.5__度.,第 8 题图) ,第 9 题图)9.(2025·南京)如图,菱形 ABCD 的面积为 120 cm2,正方形 AECF 的面积为 50 cm2,则菱形的边长为____13____cm .10.(2025·菏泽)如图,在正方形 ABCD 外作等腰直角△CDE,DE=CE,连接 BE,则tan∠EBC=________.三、解...