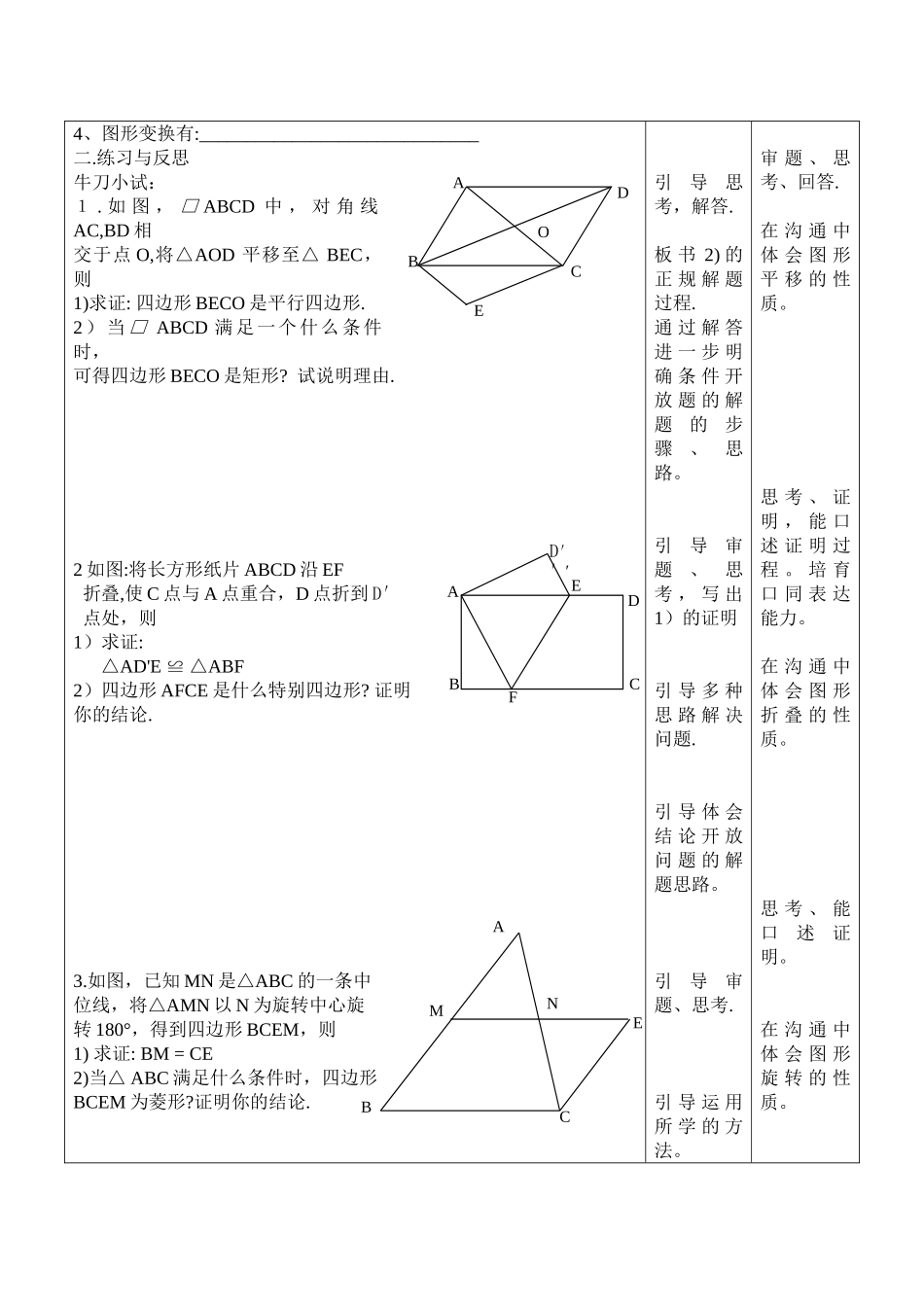
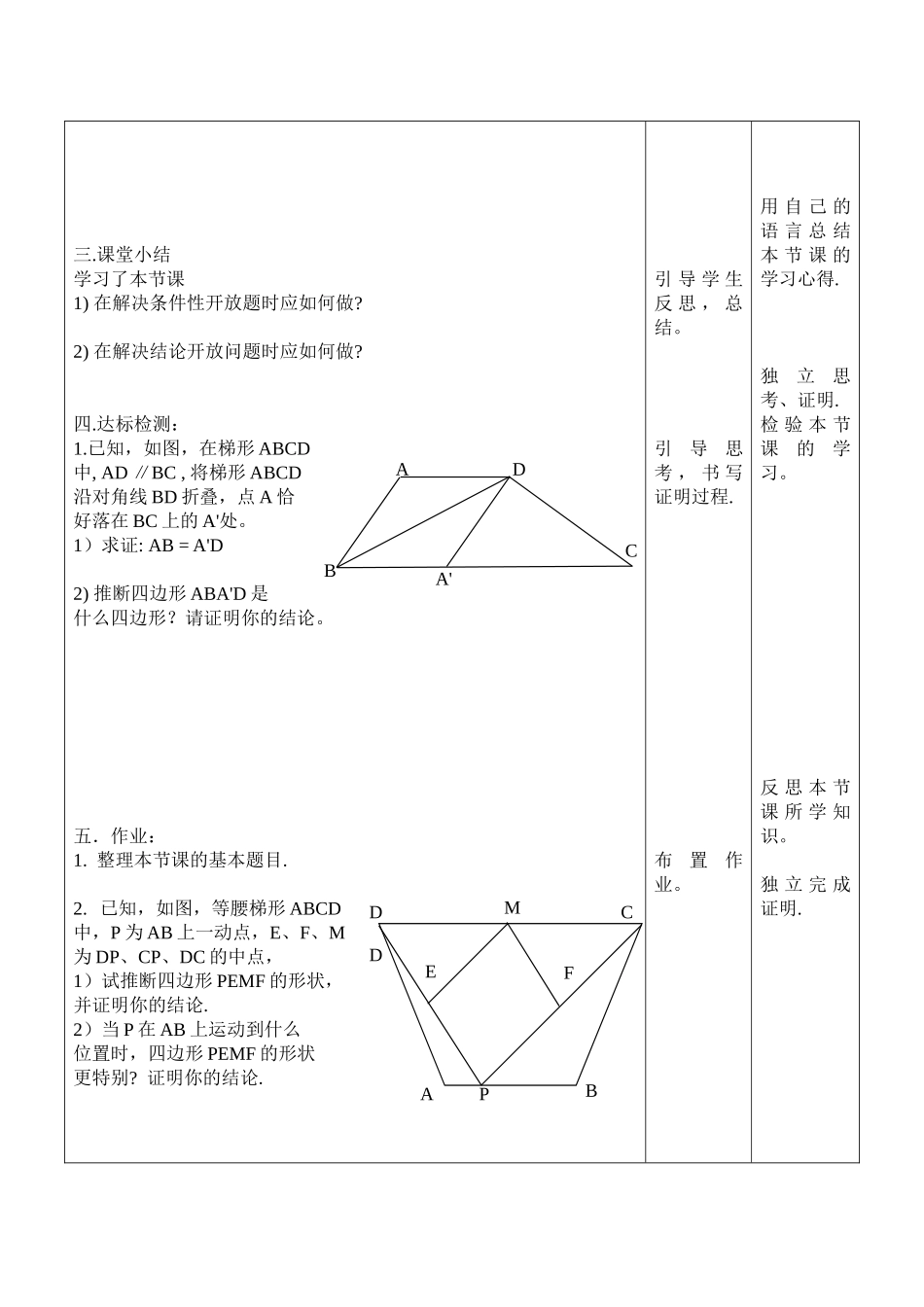
教学内容图形与证明(一)课型复习课授课人 时间 教学目标知识技能:1、熟练掌握三角形与四边形的性质与判定。 2、能综合运用知识,灵活合理选择证明方法完成题目的证明。 3、体会条件开放和结论开放性题目的解题思路。过程与方法:1、通过观察、猜想、逆推等,能给出清楚有条理的证明过程2、进一步培育学生的推理能力。情感态度与价值观:1、积极参加数学活动,在活动中体会数学的价值与有用性。2、培育学生的数学素养: 主动学习并敢于大胆猜想与质疑.教学重点三角形与四边形的性质与判定的综合应用.教学难点如何准确运用性质与判定来解决开放问题.教学设计本节课主要设计:在图形变换的条件下,解决三角形与四边形的综合开放性题目,在解决问题的同时,力求引导学生明白,结论开放的题目,从题目的条件入手,猜想结论,证明结论;条件开放的题目,从结论入手,探求出题目缺少的条件,从而添加所需条件,证明题目时,所添加的条件要当作已知条件,证出所求证的结论。同时要引导学生充分的认识图形变化的性质,灵活的选择性质解决问题。 教学方法讲练结合法、自主探究法和合作沟通法教学用具多媒体辅助教学教 学 内 容 及 过 程老师活动学生活动一.知识梳理(学生独立完成学案上的知识体系)1、证明三角形全等的方法: 全等三角形的__________相等, ________ 相等2、特别四边形的判别方法: 3、特别四边形的性质:性质边角对角线平行四边形菱形矩形正方形等腰梯形引导复习 , 观 察学情.引 导 学 生体 会 特 别四 边 形 之间的联系.回忆知识 , 为 准确 解 题 做铺垫.回 忆 特 别四 边 形 的判 别 方 法 ,并回答ABCDOEAMBCEN4、图形变换有:______________________________二.练习与反思牛刀小试:1 . 如 图 , □ ABCD 中 , 对 角 线AC,BD 相交于点 O,将△AOD 平移至△ BEC,则1)求证: 四边形 BECO 是平行四边形.2)当□ ABCD 满足一个什么条件时,可得四边形 BECO 是矩形? 试说明理由.2 如图:将长方形纸片 ABCD 沿 EF折叠,使 C 点与 A 点重合,D 点折到 D′点处,则1)求证: △AD'E ≌ △ABF2)四边形 AFCE 是什么特别四边形? 证明你的结论.3.如图,已知 MN 是△ABC 的一条中位线,将△AMN 以 N 为旋转中心旋转 180°,得到四边形 BCEM,则1) 求证: BM = CE2)当△ ABC 满足什么条件时,四边形BCEM 为菱形?证明你的结论.引导思考,解答.板...