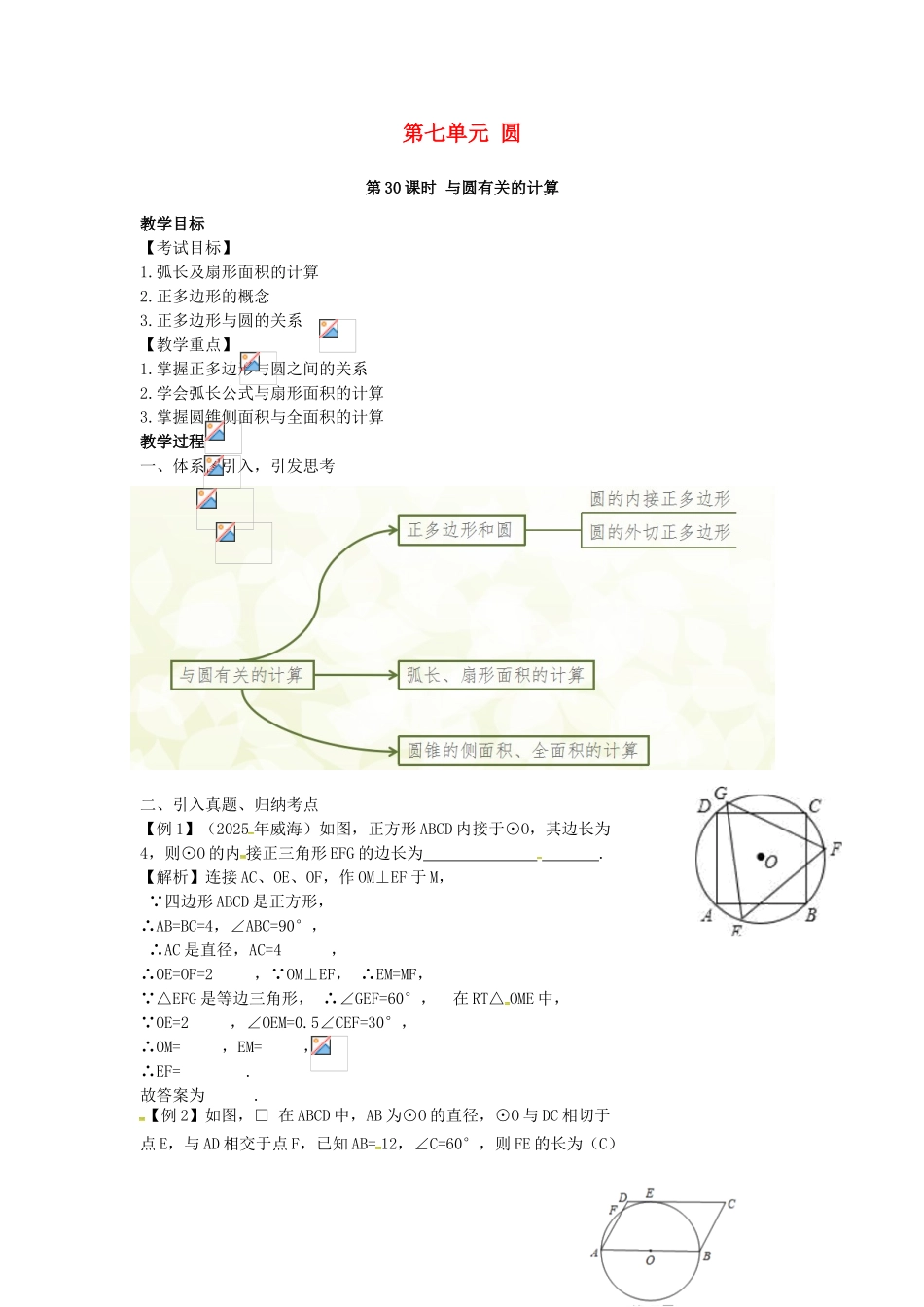
第七单元 圆第 30 课时 与圆有关的计算教学目标【考试目标】1.弧长及扇形面积的计算2.正多边形的概念3.正多边形与圆的关系【教学重点】1.掌握正多边形与圆之间的关系2.学会弧长公式与扇形面积的计算3.掌握圆锥侧面积与全面积的计算教学过程一、体系图引入,引发思考二、引入真题、归纳考点【例 1】(2025 年威海)如图,正方形 ABCD 内接于⊙O,其边长为4,则⊙O 的内 接正三角形 EFG 的边长为 .【解析】连接 AC、OE、OF,作 OM⊥EF 于 M, ∵四边形 ABCD 是正方形, ∴AB=BC=4,∠ABC=90°, ∴AC 是直径,AC=4 ,∴OE=OF=2 ,∵OM⊥EF, ∴EM=MF,∵△EFG 是等边三角形, ∴∠GEF=60°, 在 RT△ OME 中,∵OE=2 ,∠OEM=0.5∠CEF=30°,∴OM= ,EM= ,∴EF= .故答案为 .【例 2】如图,□ 在 ABCD 中,AB 为⊙O 的直径,⊙O 与 DC 相切于点 E,与 AD 相交于点 F,已知 AB= 12,∠C=60°,则 FE 的长为(C)【解析】连接 OE、OF,由切线和平行线的性 质可知∠A OE=90°.∵四边形 ABCD 是平行四边形,∴∠A=∠C=60°,∴△AOF 是等边三角形,∴∠EOF=90°- 60°=30°,OF=OA=0.5AB=6.由弧长公式,得 lFE= =π.【例 3】(2025 年宁波)如图,圆锥的底面半径 r 为 6cm, 高 h 为 8cm,则圆锥的侧面积为 (C)A.30π cm2 B.48π cm2C.60π cm2 D.80π cm2【解析】圆锥的母线长为: =10(cm),圆锥的底面圆周长为2×π×r=12π(cm).圆锥的侧面展开图是扇形,根据扇形面积公式可得 S=0.5×12π×10=60π(cm2).三、师生互动,总结知识先小组内沟通收获和感想,而后以小组为单位派代表进行总结.老师作以补充.课后作业布置作业:同步 导练教学反思学生对圆的有关计算的掌握情况很好,望多加复习巩固,做到熟练会用.