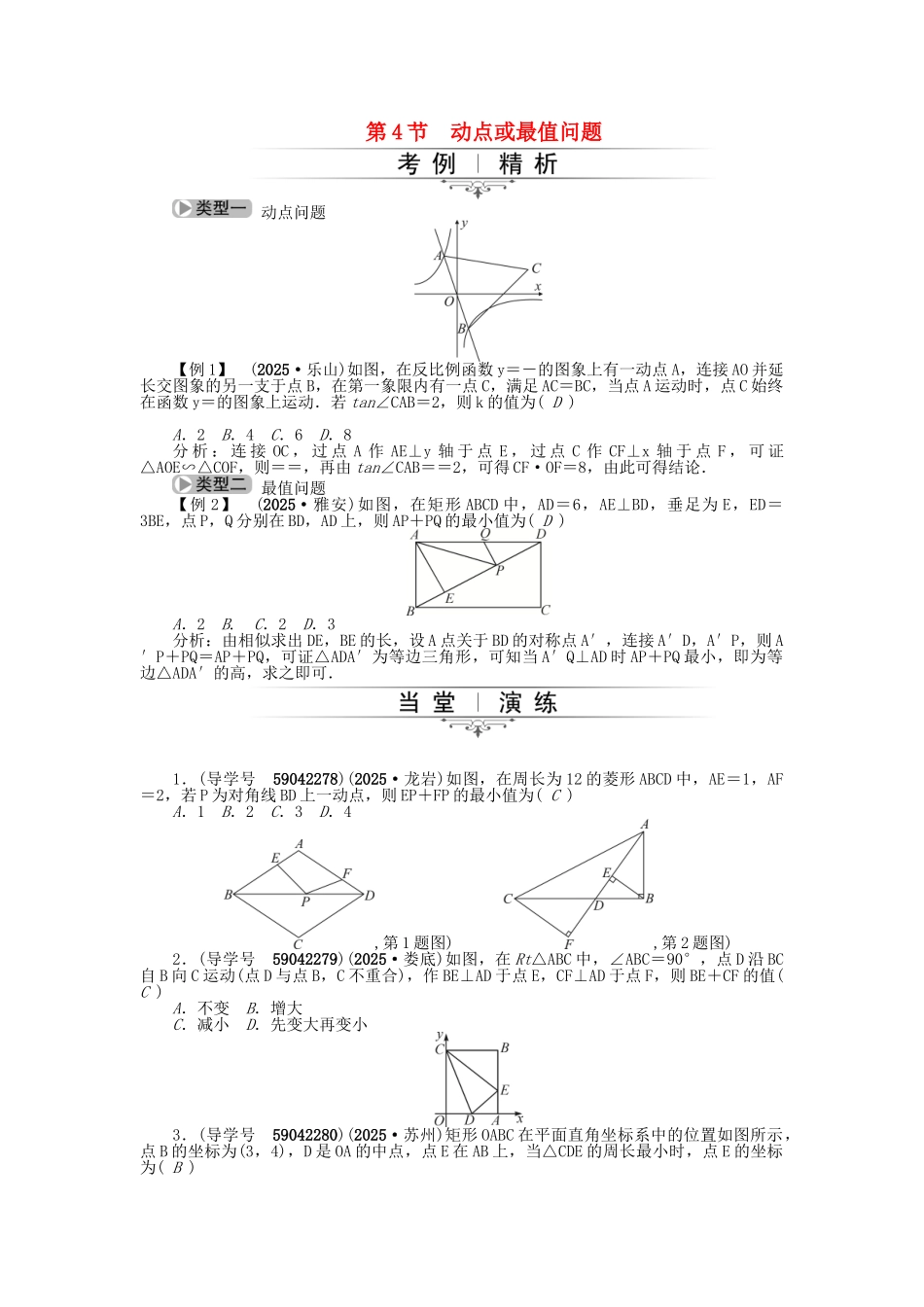
第 4 节 动点或最值问题动点问题【例 1】 (2025·乐山)如图,在反比例函数 y=-的图象上有一动点 A,连接 AO 并延长交图象的另一支于点 B,在第一象限内有一点 C,满足 AC=BC,当点 A 运动时,点 C 始终在函数 y=的图象上运动.若 tan∠CAB=2,则 k 的值为( D )A.2 B.4 C.6 D.8分 析 : 连 接 OC , 过 点 A 作 AE⊥y 轴 于 点 E , 过 点 C 作 CF⊥x 轴 于 点 F , 可 证△AOE∽△COF,则==,再由 tan∠CAB==2,可得 CF·OF=8,由此可得结论.最值问题【例 2】 (2025·雅安)如图,在矩形 ABCD 中,AD=6,AE⊥BD,垂足为 E,ED=3BE,点 P,Q 分别在 BD,AD 上,则 AP+PQ 的最小值为( D )A.2 B. C.2 D.3分析:由相似求出 DE,BE 的长,设 A 点关于 BD 的对称点 A′,连接 A′D,A′P,则 A′P+PQ=AP+PQ,可证△ADA′为等边三角形,可知当 A′Q⊥AD 时 AP+PQ 最小,即为等边△ADA′的高,求之即可. 1.(导学号 59042278)(2025·龙岩)如图,在周长为 12 的菱形 ABCD 中,AE=1,AF=2,若 P 为对角线 BD 上一动点,则 EP+FP 的最小值为( C )A.1 B.2 C.3 D.4,第 1 题图) ,第 2 题图)2.(导学号 59042279)(2025·娄底)如图,在 Rt△ABC 中,∠ABC=90°,点 D 沿 BC自 B 向 C 运动(点 D 与点 B,C 不重合),作 BE⊥AD 于点 E,CF⊥AD 于点 F,则 BE+CF 的值( C )A.不变 B.增大C.减小 D.先变大再变小3.(导学号 59042280)(2025·苏州)矩形 OABC 在平面直角坐标系中的位置如图所示,点 B 的坐标为(3,4),D 是 OA 的中点,点 E 在 AB 上,当△CDE 的周长最小时,点 E 的坐标为( B )A.(3,1) B.(3,) C.(3,) D.(3,2)4.(导学号 59042281)(2025·贵港)如图,抛物线 y=-x2+x+与 x 轴交于 A,B 两点,与 y 轴交于点 C.若点 P 是线段 AC 上方的抛物线上一动点,当△ACP 的面积取得最大值时,点 P的坐标是( B )A.(4,3) B.(5,)C.(4,) D.(5,3)5 . ( 导 学 号 59042282)(2025· 泸 州 ) 如 图 , 在 平 面 直 角 坐 标 系 中 , 已 知 点A(1,0),B(1-a,0),C(1+a,0)(a>0),点 P 在以 D(4,4)为圆心,1 为半径的圆上运动,且始终满足∠BPC=90°,则 a 的最大值是__6__.,第 5 题图) ...