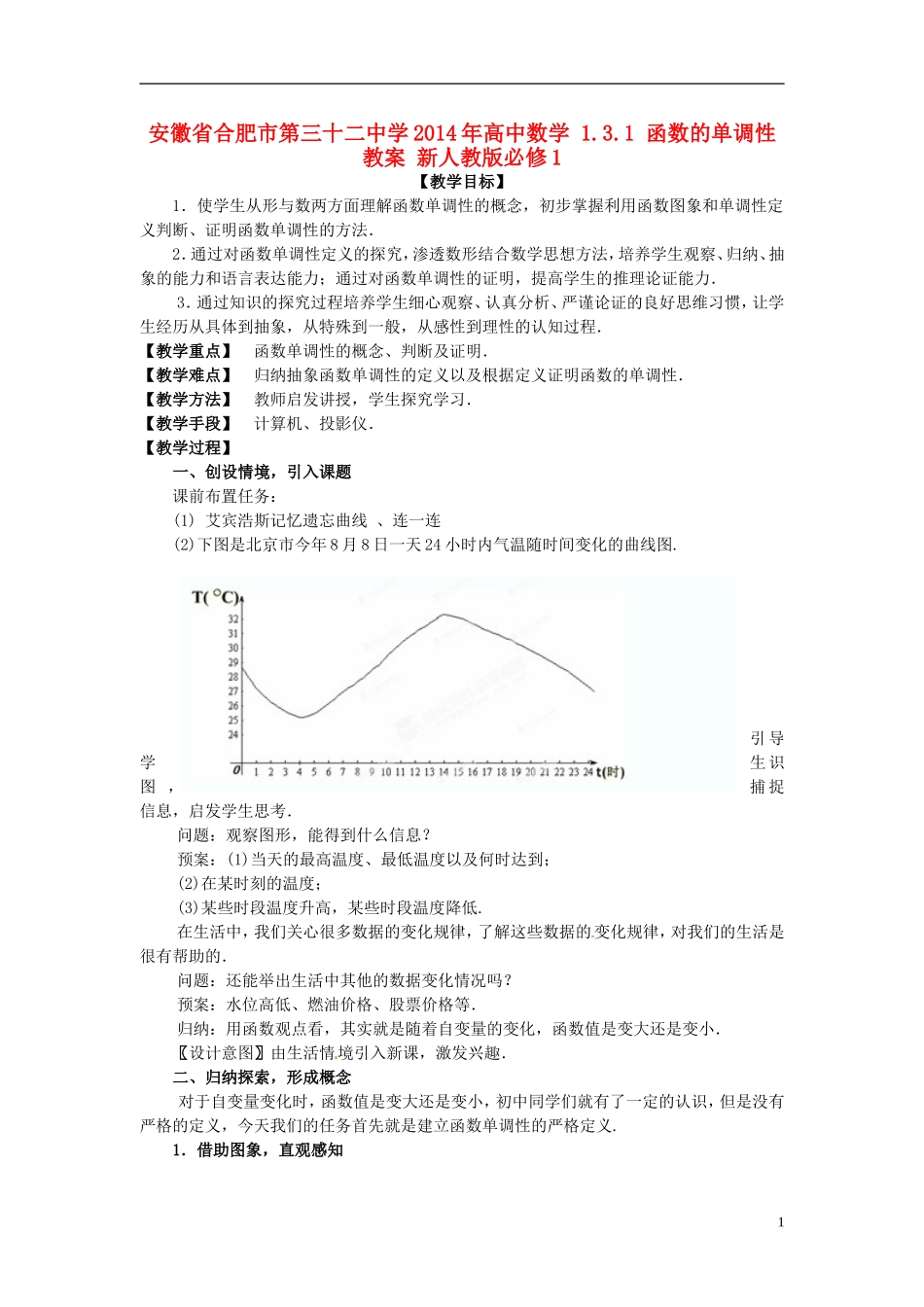
安徽省合肥市第三十二中学 2014 年高中数学 1.3.1 函数的单调性教案 新人教版必修 1【教学目标】1.使学生从形与数两方面理解函数单调性的概念,初步掌握利用函数图象和单调性定义判断、证明函数单调性的方法.2.通过对函数单调性定义的探究,渗透数形结合数学思想方法,培养学生观察、归纳、抽象的能力和语言表达能力;通过对函数单调性的证明,提高学生的推理论证能力. 3.通过知识的探究过程培养学生细心观察、认真分析、严谨论证的良好思维习惯,让学生经历从具体到抽象,从特殊到一般,从感性到理性的认知过程.【教学重点】 函数单调性的概念、判断及证明.【教学难点】 归纳抽象函数单调性的定义以及根据定义证明函数的单调性.【教学方法】 教师启发讲授,学生探究学习.【教学手段】 计算机、投影仪.【教学过程】一、创设情境,引入课题课前布置任务:(1) 艾宾浩斯记忆遗忘曲线 、连一连 (2)下图是北京市今年 8 月 8 日一天 24 小时内气温随时间变化的曲线图.引 导学生 识图 ,捕 捉信息,启发学生思考.问题:观察图形,能得到什么信息?预案:(1)当天的最高温度、最低温度以及何时达到;(2)在某时刻的温度;(3)某些时段温度升高,某些时段温度降低.在生活中,我们关心很多数据的变化规律,了解这些数据的变化规律,对我们的生活是很有帮助的.问题:还能举出生活中其他的数据变化情况吗?预案:水位高低、燃油价格、股票价格等.归纳:用函数观点看,其实就是随着自变量的变化,函数值是变大还是变小.〖设计意图〗由生活情境引入新课,激发兴趣.二、归纳探索,形成概念对于自变量变化时,函数值是变大还是变小,初中同学们就有了一定的认识,但是没有严格的定义,今天我们的任务首先就是建立函数单调性的严格定义.1.借助图象,直观感知1OOOyyyyxxxx1 2 3-1-2-3-1-2-31231 2 3-1-2-3-11234561 2 3-1-2-1-212341 2-1-2-3-112345OO12345612345xy问题 1:分别作出函数的图象,并且观察自变量变化时,函数值有什么变化规律?预案:(1)函数在整个定义域内 y 随 x 的增大而增大;函数在整个定义域内 y 随 x 的增大而减小.(2)函数在上 y 随 x 的增大而增大,在上 y 随 x 的增大而减小.(3)函数在上 y 随 x 的增大而减小,在上 y 随 x 的增大而减小.引导学生进行分类描述 (增函数、减函数).同时明确函数的单调性是对定义域内某个区间而言的,是函数的局部性质.问题 2:能不...