北京四中高中数学 指数与指数幂的运算提高知识讲解 新人教A版必修1

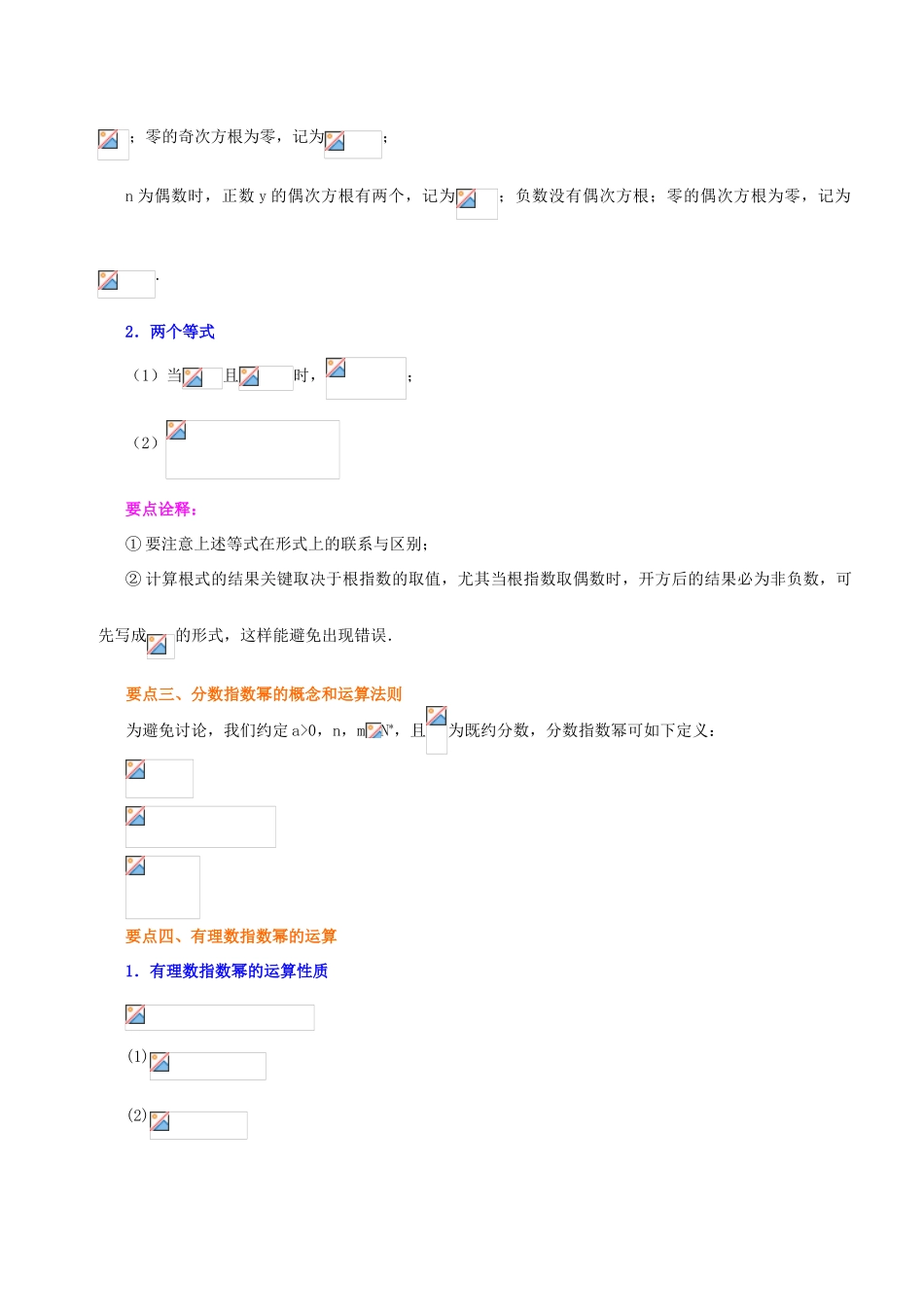
指数与指数幂的运算 【学习目标】1.理解分数指数的概念，掌握有理指数幂的运算性质(1)理解 n 次方根，n 次根式的概念及其性质，能根据性质进行相应的根式计算； (2)能认识到分数指数是指数概念由整数向有理数的一次推广，了解它是根式的一种新的写法，能正确进行根式与分数指数幂的互化；(3)能利用有理指数运算性质简化根式运算. 2.掌握无理指数幂的概念，将指数的取值范围推广到实数集；3.通过指数范围的扩大，我们要能理解运算的本质，认识到知识之间的联系和转化，认识到符号化思想的重要性，在抽象的符号或字母的运算中提高运算能力；4.通过对根式与分数指数幂的关系的认识，能学会透过表面去认清事物的本质．【要点梳理】要点一、整数指数幂的概念及运算性质1．整数指数幂的概念2．运算法则（1）；（2）；（3）；（4）.要点二、根式的概念和运算法则1．n 次方根的定义：若 xn=y(n∈N*，n>1，y∈R)，则 x 称为 y 的 n 次方根.n 为奇数时，正数 y 的奇次方根有一个，是正数，记为；负数 y 的奇次方根有一个，是负数，记为；零的奇次方根为零，记为；n 为偶数时，正数 y 的偶次方根有两个，记为；负数没有偶次方根；零的偶次方根为零，记为.2．两个等式（1）当且时，；（2）要点诠释：① 要注意上述等式在形式上的联系与区别；② 计算根式的结果关键取决于根指数的取值，尤其当根指数取偶数时，开方后的结果必为非负数，可先写成的形式，这样能避免出现错误．要点三、分数指数幂的概念和运算法则为避免讨论，我们约定 a>0，n，mN*，且为既约分数，分数指数幂可如下定义：要点四、有理数指数幂的运算1．有理数指数幂的运算性质(1) (2) (3)当 a>0，p 为无理数时，ap是一个确定的实数，上述有理数指数幂的运算性质仍适用.要点诠释：(1)根式问题常利用指数幂的意义与运算性质，将根式转化为分数指数幂运算；(2)根式运算中常出现乘方与开方并存，要注意两者的顺序何时可以交换、何时不能交换 .如；(3)幂指数不能随便约分.如.2.指数幂的一般运算步骤有括号先算括号里的；无括号先做指数运算．负指数幂化为正指数幂的倒数．底数是负数，先确定符号，底数是小数，先要化成分数，底数是带分数，先要化成假分数，然后要尽可能用幂的形式表示，便于用指数运算性质．在化简运算中，也要注意公式：a2－b2＝（a－b）（a＋b），（a±b）2＝a2±2ab＋b2，（a±b）3＝a3±3a2b＋3ab2±b3，a3－b3＝（a－b）（a2＋ab＋b2），a3＋b3＝...