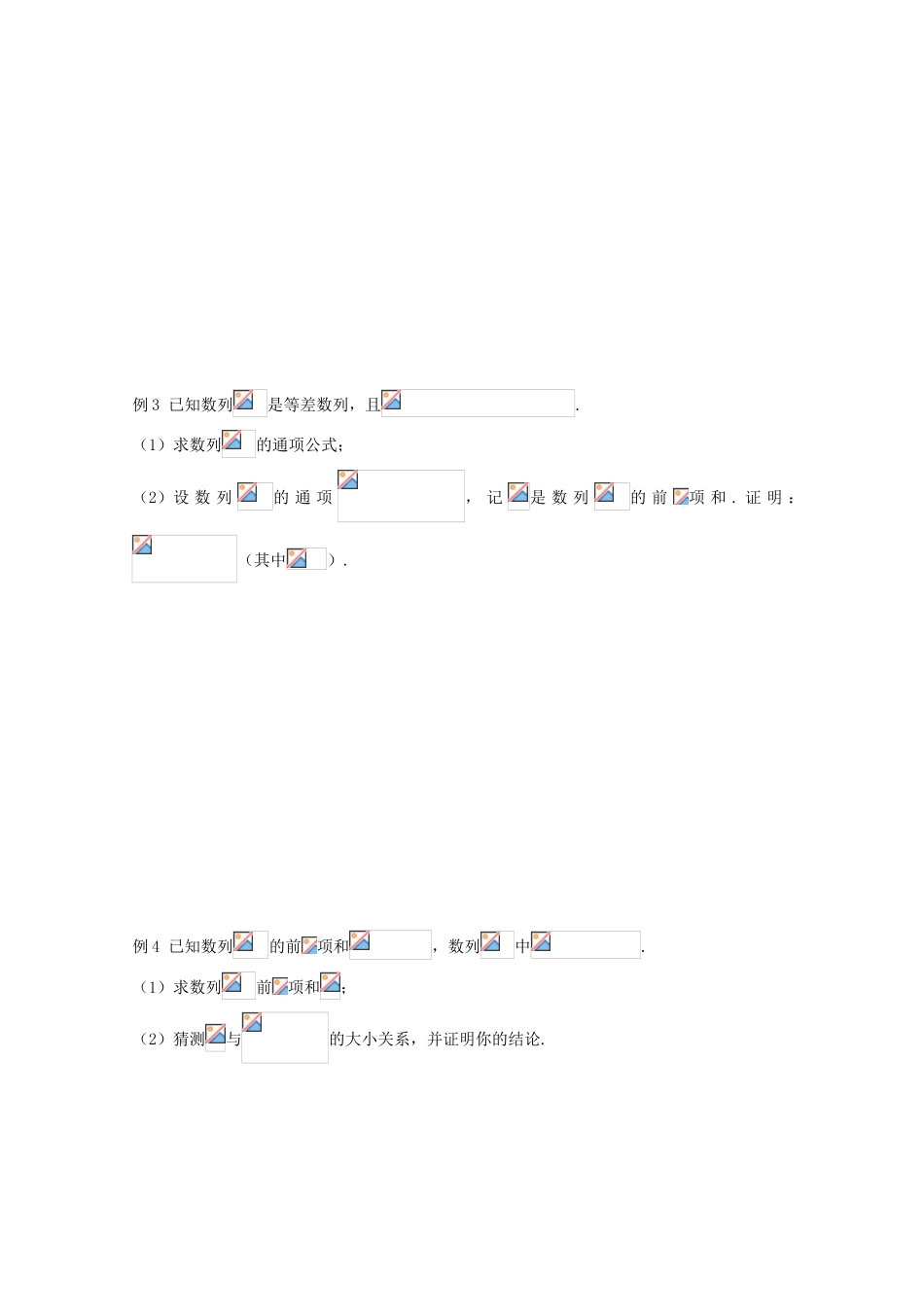
第十二讲 数列大题讲解(2) 1.数列放缩法的应用例 1 设 数 列的 前项 和 为, 对 任 意, 都 有 , 且 满 足.(1)数列的通项公式;(2)当时,设,数列的前项和,求证:.例 2 数列满足,当时,.(1)证明:数列为等比数列,并求数列的通项公式;(2)试比较与的大小,并说明理由.例 3 已知数列是等差数列,且.(1)求数列的通项公式;(2)设 数 列的 通 项, 记是 数 列的 前项 和 . 证 明 :(其中).例 4 已知数列的前项和,数列中.(1)求数列前项和;(2)猜测与的大小关系,并证明你的结论.例 5 已知等差数列的前项和为,公差,,且成等比数列.(1)求的前项和为;( 2 ) 设, 且, 数 列的 前项 和 为, 求 证 :.2. 数列新型题例 1 已知等差数列()中,.(1)求数列的通项公式;(2)若 将 数 列中 的 项 重 新 组 合 , 得 到 新 数 列, 具 体 方 法 如 下 :依 次 类 推 , 第项是中相应的项的和,求数列的前项和.3.奇偶分类数列例 1 已知数列满足: (1)数列是否为等差数列或等比数列?说明理由;(2)求证数列是等差数列,并求的通项公式;(3)设,求数列的前项和.例 2 . 已 知 数 列, 且, , 其 中 k=1,2,3,…….(1)求;(2)求的通项公式.例 3【2011 年合肥一模文】已知以 1 为首项的数列满足:(1)写出,并求出的通项公式;(2)设数列前 n 项和,求数列前 n 项和.例 4【2012 年合肥六中最后一卷理】已知数列满足,前 n 项和为, (1)若满足,求前 n 项和;(2)若等比数列满足,求 p 的值;(3)当时,问是否存在,使得,若存在,求出所有的 n 的值;若不存在,请说明理由.4.数列综合题21.(本小题满分 14 分)已知曲线 ,过上一点作一斜率的直线交曲线 C 于另一点,其中(1)求与之间的关系式;(2)求证:数列是等比数列;(3)求证:21.解:(1)直线方程为,.……………………4 分(2)设由(1)得又是等比数列; ……………………8 分(3)由(2)得 ……………………10 分当 n 为偶数时,则; ………12 分当 n 为奇数时,则而综上所述,当时,成立. ………14 分21. (本小题满分 14 分)已知数列满足:(其中常数).(Ⅰ)求数列的通项公式;(Ⅱ)求证:当时,数列中的任何三项都不可能成等比数列;(Ⅲ)设为数列的前项和.求证:若任意,21.解:(Ⅰ)当 n...