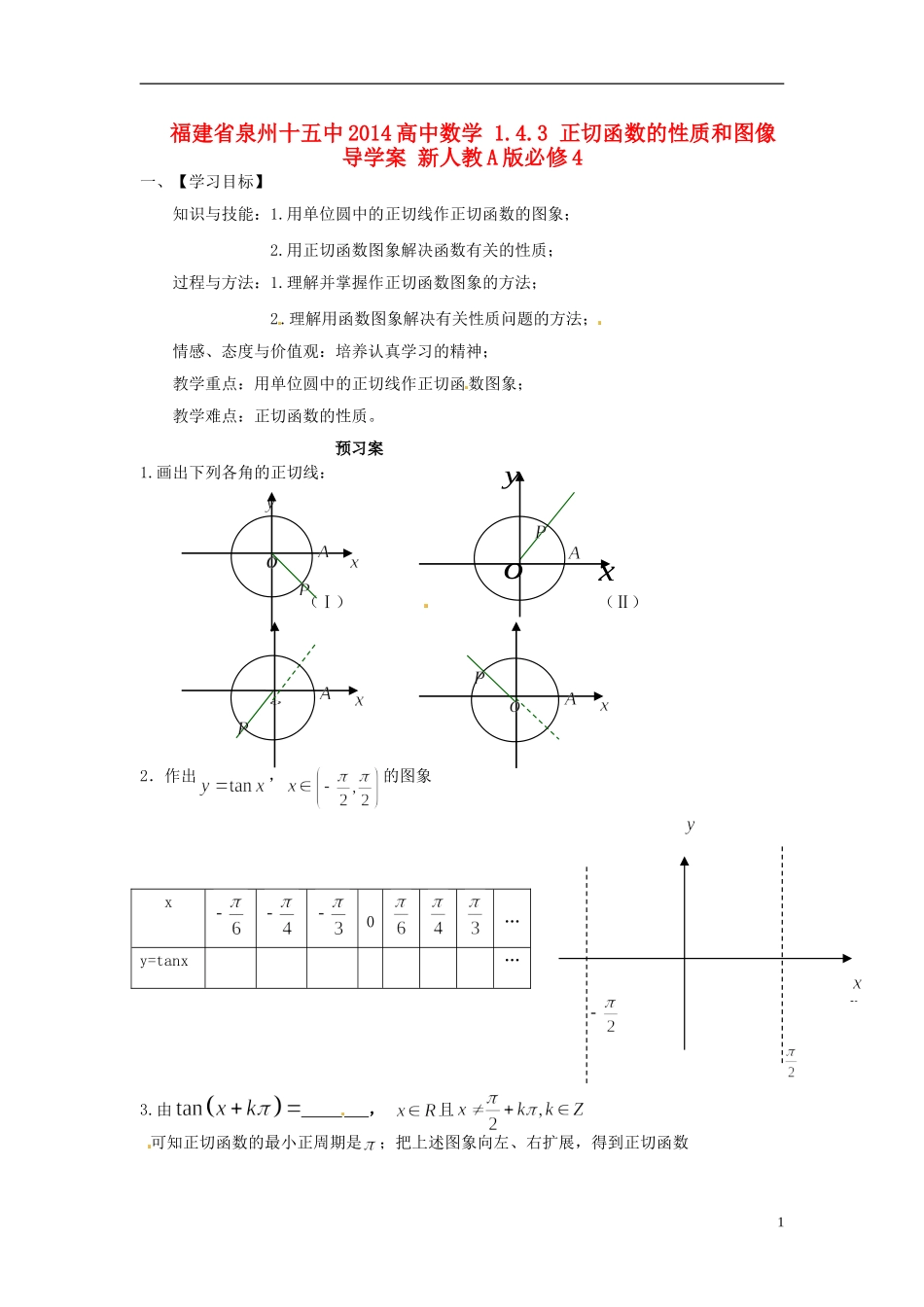
福建省泉州十五中 2014 高中数学 1.4.3 正切函数的性质和图像导学案 新人教 A 版必修 4一、【学习目标】知识与技能:1.用单位圆中的正切线作正切函数的图象;2.用正切函数图象解决函数有关的性质;过程与方法:1.理解并掌握作正切函数图象的方法;2.理解用函数图象解决有关性质问题的方法; 情感、态度与价值观:培养认真学习的精神; 教学重点:用单位圆中的正切线作正切函数图象; 教学难点:正切函数的性质。预习案1.画出下列各角的正切线: (Ⅰ) (Ⅱ) 2.作出,的图象 x0…y=tanx… 3.由 , 且可知正切函数的最小正周期是;把上述图象向左、右扩展,得到正切函数1xyoyx,且的图象,称“ ”。在下面直角坐标系中,作出正切函数图象?由图象可以看出,正切曲线是由被相互平行的直线所隔开的无穷多支曲线组成的。探究案1、正切函数的定义域 。2、正切函数的周期性函数()是 函数,且它的周期是 .一般结论:函数的周期 T= .3、正切函数的奇偶性因 为 () 所 以 正 切 函 数()是 函数.函数图象关于 对称. 4、正切函数的单调性由正切线的变化规律可以得出,正切函数在内是 函数,又由正切函数的周期性可知,正切函数在开区间 内都是增函数。正切函数在整个定义域上 (填是或不是)递增函数。5、 正切函数的值域由图(Ⅰ)可知,当大于且无限接近于时,正切线向轴的 方向无限20y延伸;当小于且无限接近于时,正切线向轴的 方向无限延伸.因此,在内可以取任意实数,但没有最大值、最小值.因此,正切函数的值域是 . 训练案1.y=tan(3x+1)的最小正周期是________2.若 tanx=-且 x∈(-,),则 x=________3.判断奇偶性:y=tanx+是______函数4.判断大小:tan(-)______tan(-),tan______tan5.下列函数中,既是以 π 为周期的奇函数,又是(0,)上的增函数的是( )A. y=tanx B. y=tanωx (ω>0 且 ω≠1) C. y=tan D. y=|sinx|6. 函数的周期是 ( ) A. B.-3π C. D.3π7. 函数的定义域是 ( ) A. B.C. D.8.求函数的定义域。9.求函数的值域。310.求函数的定义域 、周期和单调区间。反思:4