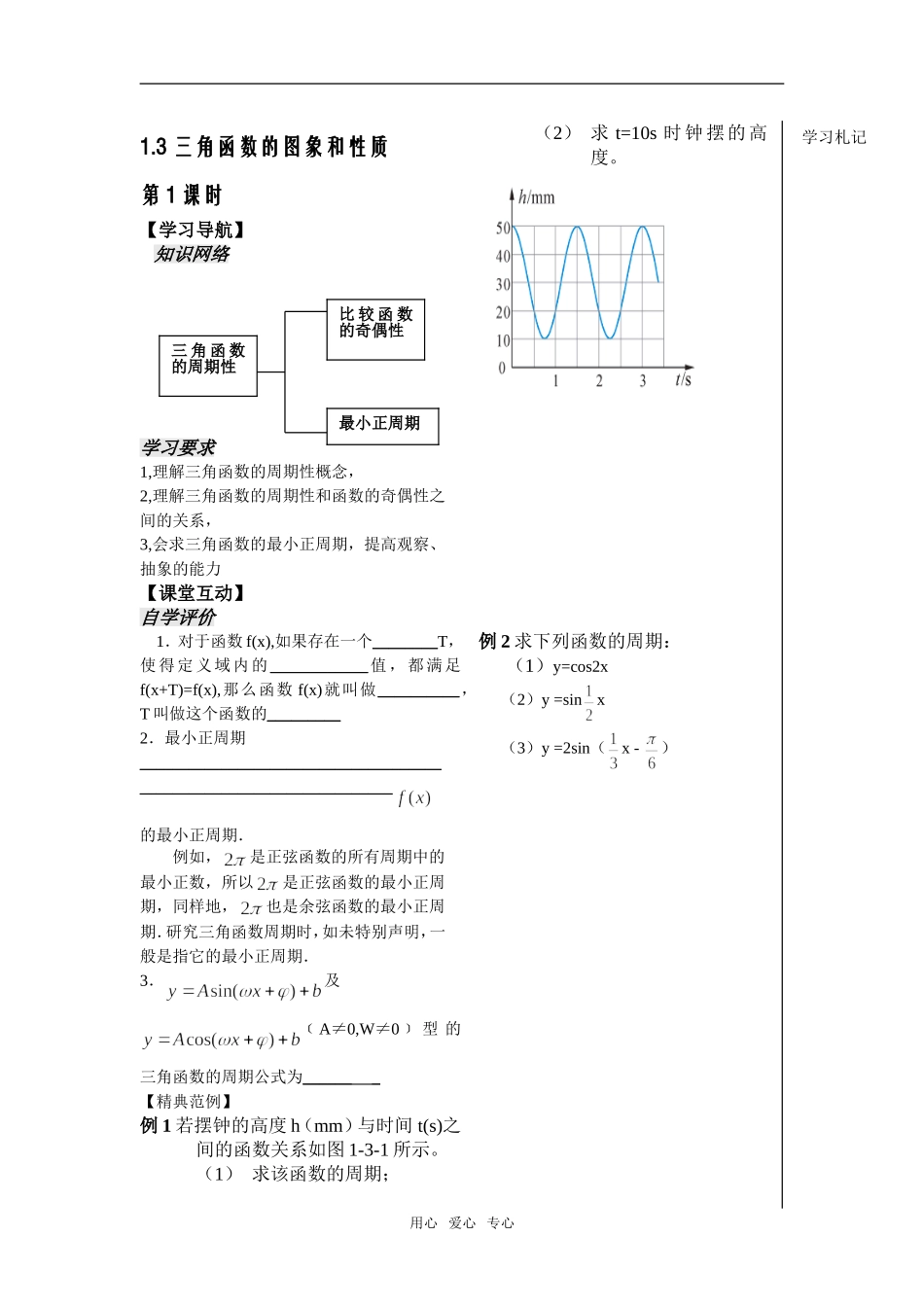
1.3 三角函数的图象和性质第 1 课时【学习导航】 知识网络学习要求 1,理解三角函数的周期性概念,2,理解三角函数的周期性和函数的奇偶性之间的关系,3,会求三角函数的最小正周期,提高观察、抽象的能力【课堂互动】自学评价1.对于函数 f(x),如果存在一个________T,使得定义域内的____________值,都满足f(x+T)=f(x),那么函数 f(x)就叫做__________,T 叫做这个函数的_________2.最小正周期____________________________________________________________________的最小正周期. 例如,是正弦函数的所有周期中的最小正数,所以是正弦函数的最小正周期,同样地,也是余弦函数的最小正周期.研究三角函数周期时,如未特别声明,一般是指它的最小正周期.3.及﹝A≠0,W≠0﹞ 型 的三角函数的周期公式为______ _【精典范例】例 1 若摆钟的高度 h(mm)与时间 t(s)之间的函数关系如图 1-3-1 所示。(1) 求该函数的周期;(2) 求 t=10s 时钟摆的高度。例 2 求下列函数的周期:(1)y=cos2x (2)y =sinx (3)y =2sin(x - )用心 爱心 专心三 角 函 数的周期性比 较 函 数的奇偶性最小正周期学习札记例 3 已 知 函 数( ),yf x xR, 满 足(2)( )f xf x对于一切 xR都成立,求证:4 是( )f x 的一个周期. 追踪训练1.求下列函数的周期:2.若函数的最小正周期为,求正数k的值.3.若弹簧振子对平衡位置的位移(mm)与时间t(s)之间的函数关系如图所示:(1)求该函数的周期;(2)求t=10.5 s时弹簧振子对平衡位置的位移用心 爱心 专心学习札记【师生互动】用心 爱心 专心学生质疑教师释疑