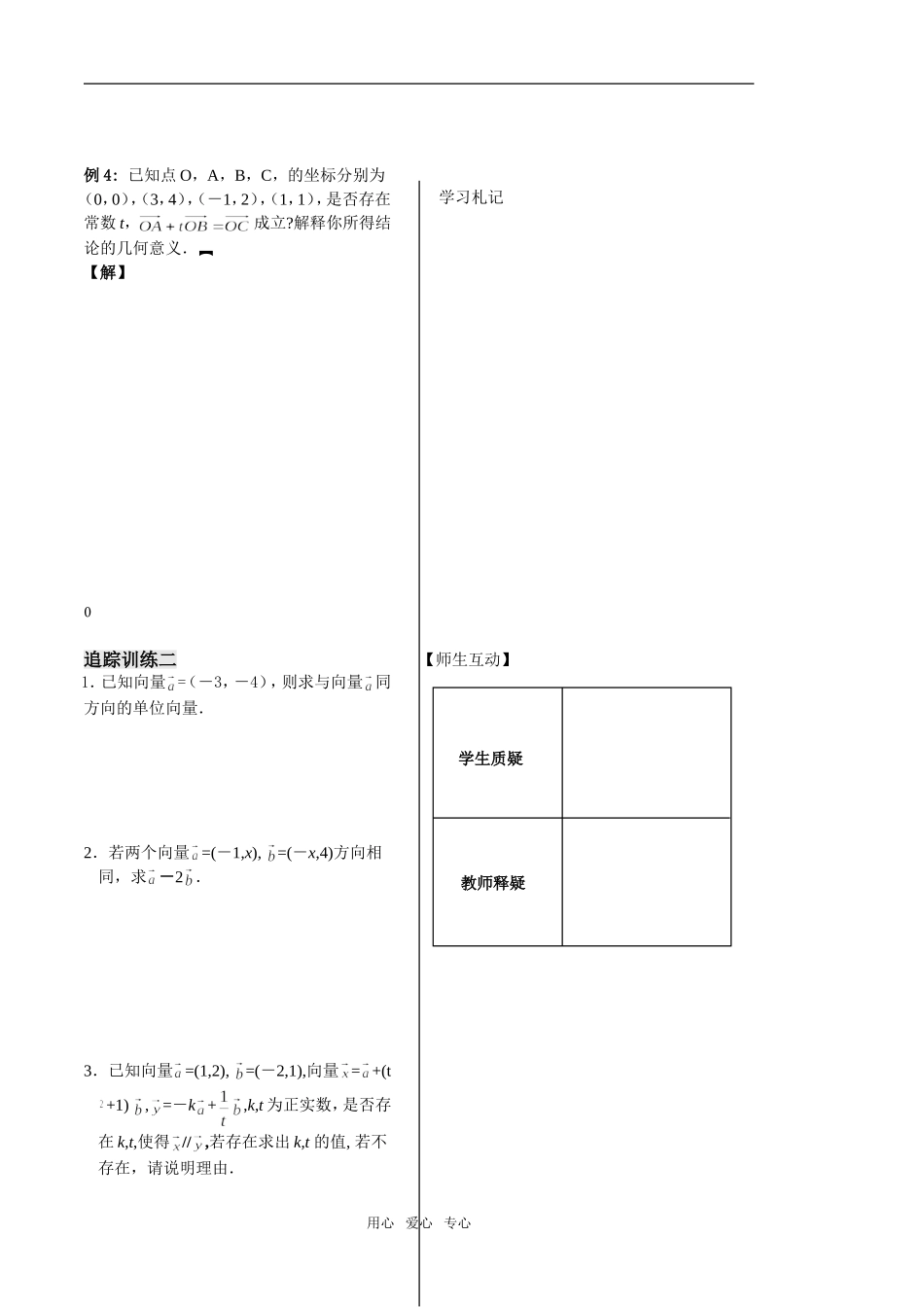
第 3 课时 【学习导航】 知识网络 学习要求 1.进一步掌握向量的坐标表示;2.理解向量平行坐标表示的推导过程;3.提高运用向量的坐标表示解决问题的能力.【课堂互动】自学评价1.向量平行的线性表示是:_______________ 2.向量平行的坐标表示是:设 =(,), =(,)(),如果 ∥ ,那么__________________,反之也成立.3 . 已 知 A , B , C , O 四 点 满 足 条 件 :,则能得到______________________【精典范例】例 1:已知 A(-1,0),B(3,-1),C(1,2),并且求证:.【解】例 2:已知 =(1,0), =(2,1),当实数 k 为何值时,向量 k - 与 +3 平行?并确定此时它们是同向还是反向.【解】例 3:如图,已知 A(4,0),B(4,4),C(2,6),求 AC和 OB 交点 P 的坐标.【解】追踪训练一1. 已知向量 =(2,3), =(6,y),且 // ,求实数 y的值.2. 已知,平行四边形 ABCD 的三个顶点的坐标分别为 A(2,1),B(-1,3),C(3,4),求第四个顶点 D 的坐标.3. 已知 A(0,-2),B(2,2),C(3,4),求证:A ,B,C 三点共线.用心 爱心 专心AAPOCB向量平行表示应用线性表示坐标表示三点共线学习札记例 4: 已知点 O,A,B,C,的坐标分别为(0,0),(3,4),(-1,2),(1,1),是否存在常数 t,成立?解释你所得结论的几何意义.【解】追踪训练二1.已知向量 =(-3,-4),则求与向量 同方向的单位向量.2.若两个向量 =(-1,x), =(-x,4)方向相同,求 -2 .3.已知向量 =(1,2), =(-2,1),向量 = +(t+1) ,=-k +,k,t 为正实数,是否存在 k,t,使得 //,若存在求出 k,t 的值, 若不存在,请说明理由. 【师生互动】用心 爱心 专心学生质疑教师释疑学习札记