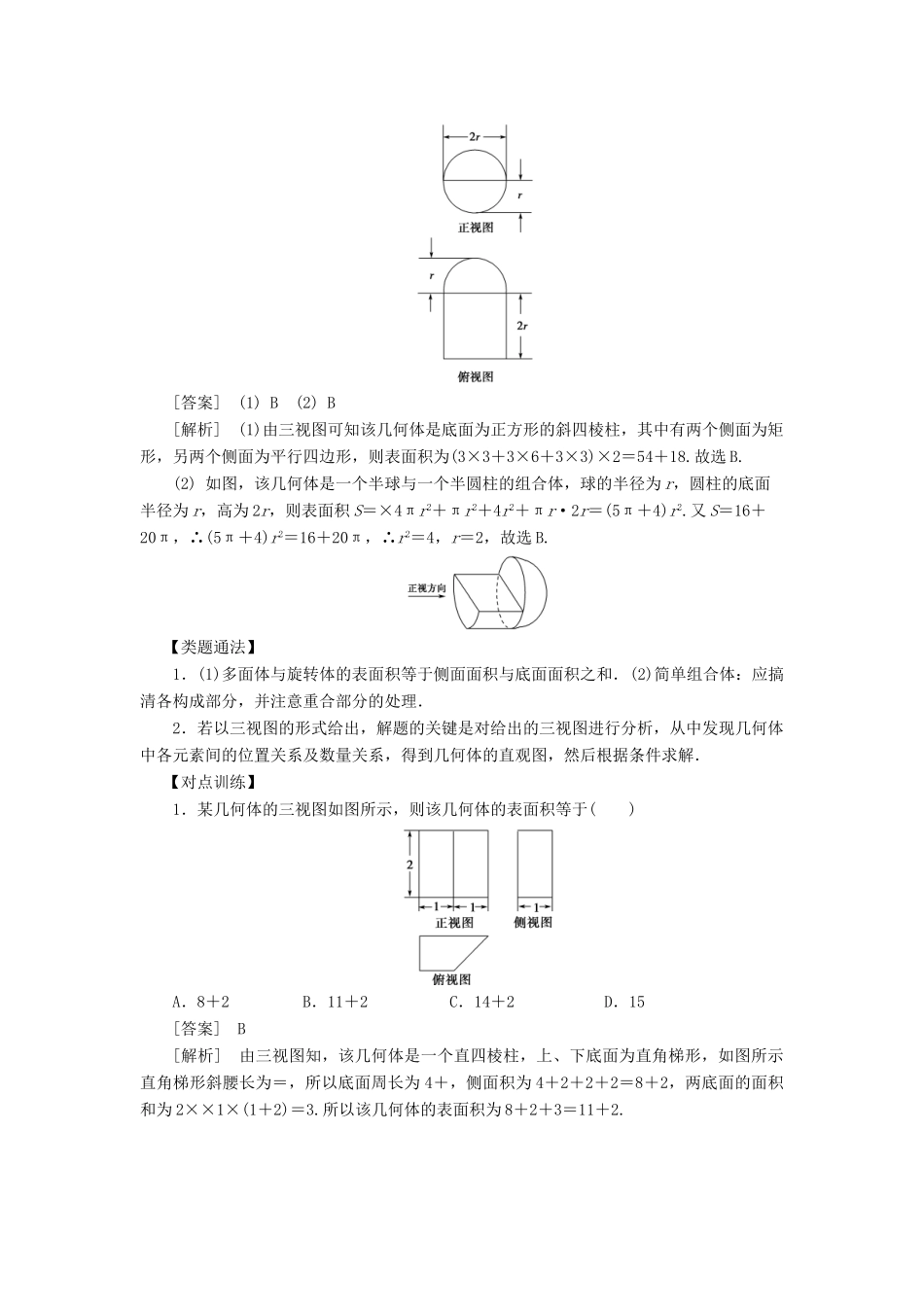
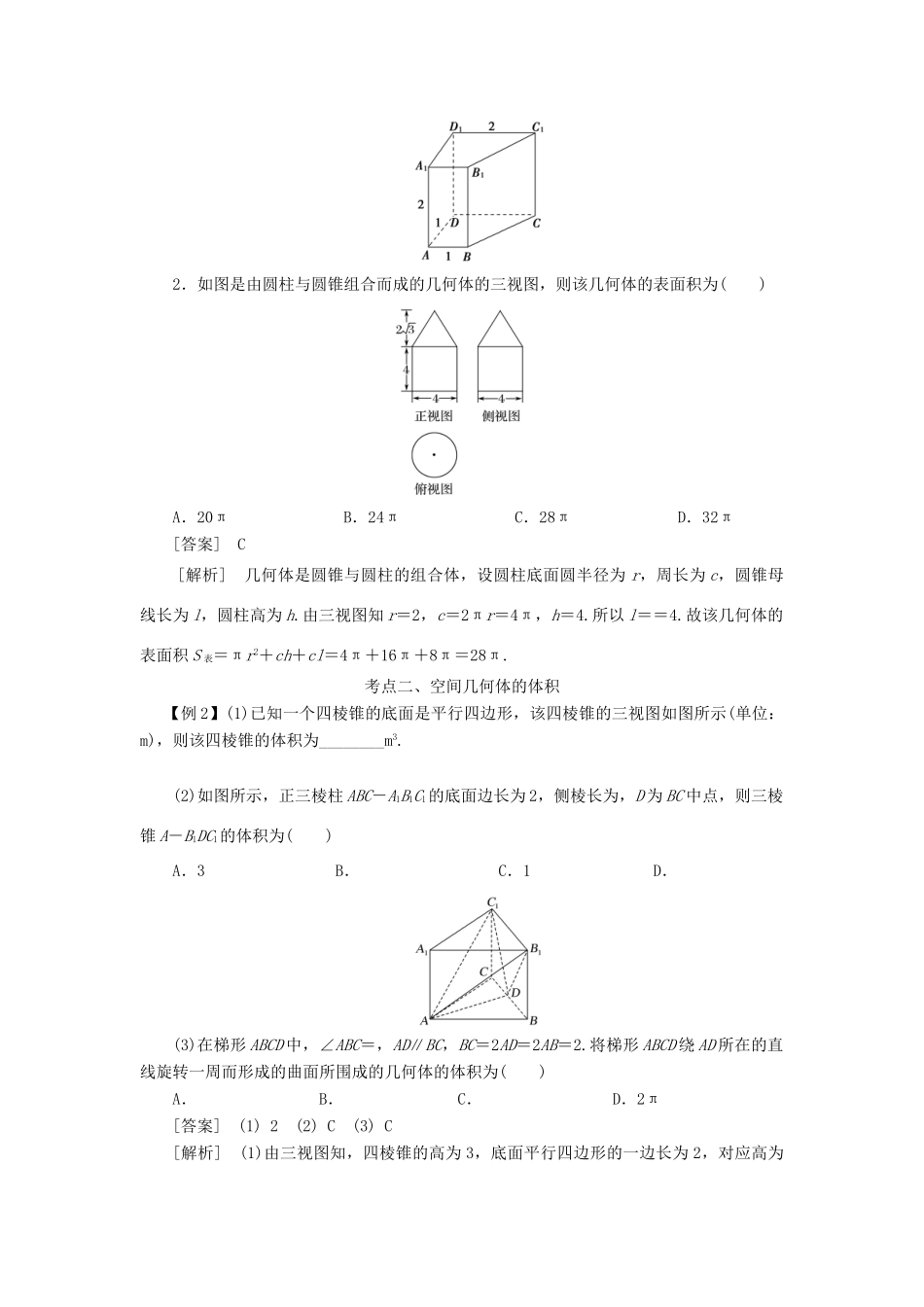
空间几何体的表面积与体积【考点梳理】1.多面体的表(侧)面积因为多面体的各个面都是平面,所以多面体的侧面积就是所有侧面的面积之和,表面积是侧面积与底面面积之和.2.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=2πrlS 圆锥侧=π rl S 圆台侧=π( r 1+ r 2) l 3.柱、锥、台和球的表面积和体积名称几何体表面积体积柱体(棱柱和圆柱)S 表面积=S 侧+2S 底V=Sh锥体(棱锥和圆锥)S 表面积=S 侧+S 底V=Sh台体(棱台和圆台)S 表面积=S 侧+S 上+S 下V=(S 上+S 下+)h球S=4π R 2 V=πR3【考点突破】考点一、空间几何体的表面积【例 1】(1)如图,网格纸上小正方形的边长为 1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )A.18+36 B.54+18 C.90 D.81(2)圆柱被一个平面截去一部分后与半球(半径为 r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为 16+20π,则 r=( )A.1 B.2 C.4 D.8[答案] (1) B (2) B[解析] (1)由三视图可知该几何体是底面为正方形的斜四棱柱,其中有两个侧面为矩形,另两个侧面为平行四边形,则表面积为(3×3+3×6+3×3)×2=54+18.故选 B.(2) 如图,该几何体是一个半球与一个半圆柱的组合体,球的半径为 r,圆柱的底面半径为 r,高为 2r,则表面积 S=×4πr2+πr2+4r2+πr·2r=(5π+4)r2.又 S=16+20π,∴(5π+4)r2=16+20π,∴r2=4,r=2,故选 B.【类题通法】1.(1)多面体与旋转体的表面积等于侧面面积与底面面积之和.(2)简单组合体:应搞清各构成部分,并注意重合部分的处理.2.若以三视图的形式给出,解题的关键是对给出的三视图进行分析,从中发现几何体中各元素间的位置关系及数量关系,得到几何体的直观图,然后根据条件求解.【对点训练】1.某几何体的三视图如图所示,则该几何体的表面积等于( )A.8+2 B.11+2 C.14+2 D.15[答案] B[解析] 由三视图知,该几何体是一个直四棱柱,上、下底面为直角梯形,如图所示直角梯形斜腰长为=,所以底面周长为 4+,侧面积为 4+2+2+2=8+2,两底面的面积和为 2××1×(1+2)=3.所以该几何体的表面积为 8+2+3=11+2.2.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A.20π B.24π C.28π D.32π[答案] C[解析] 几何体是圆锥与圆柱...