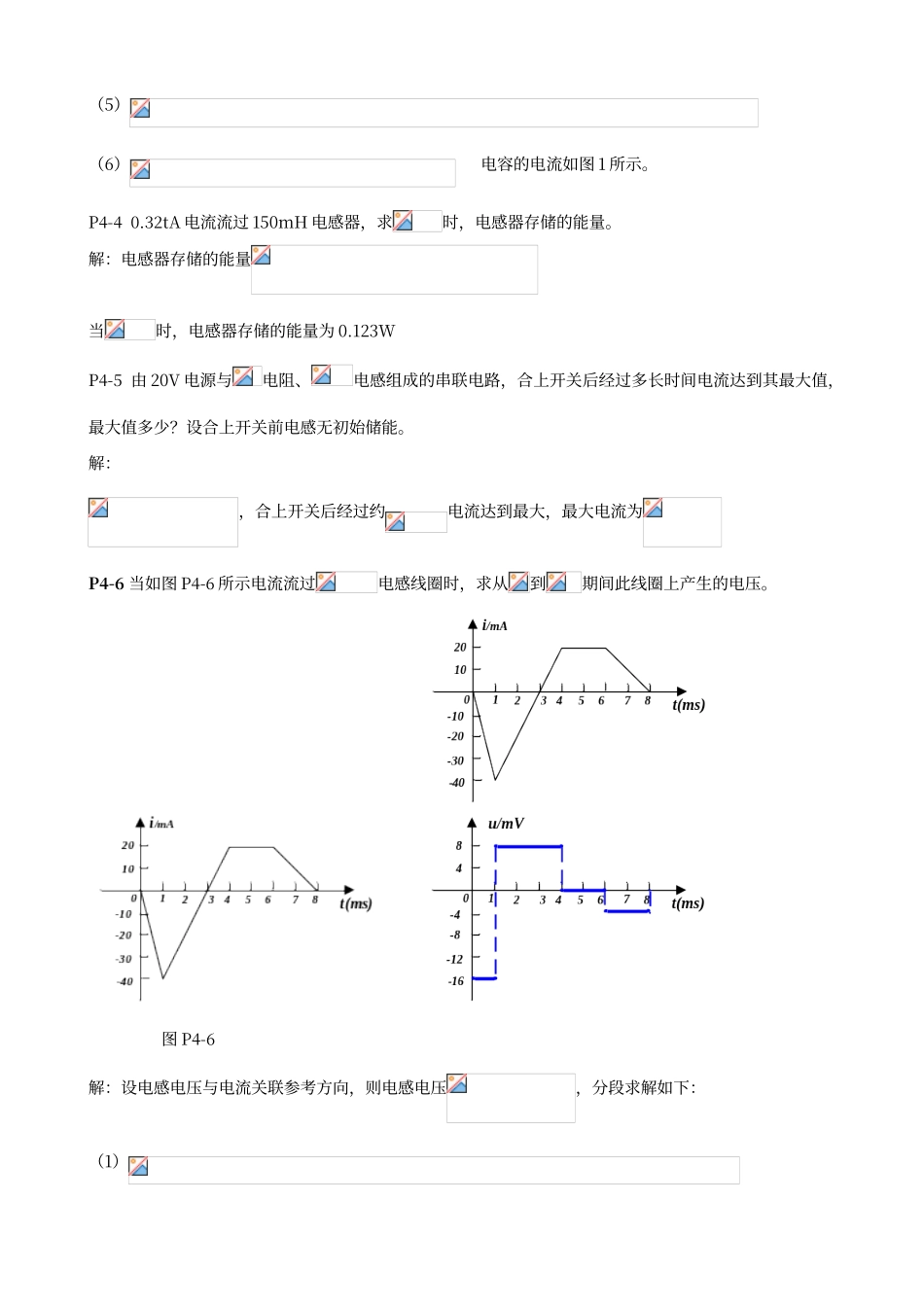
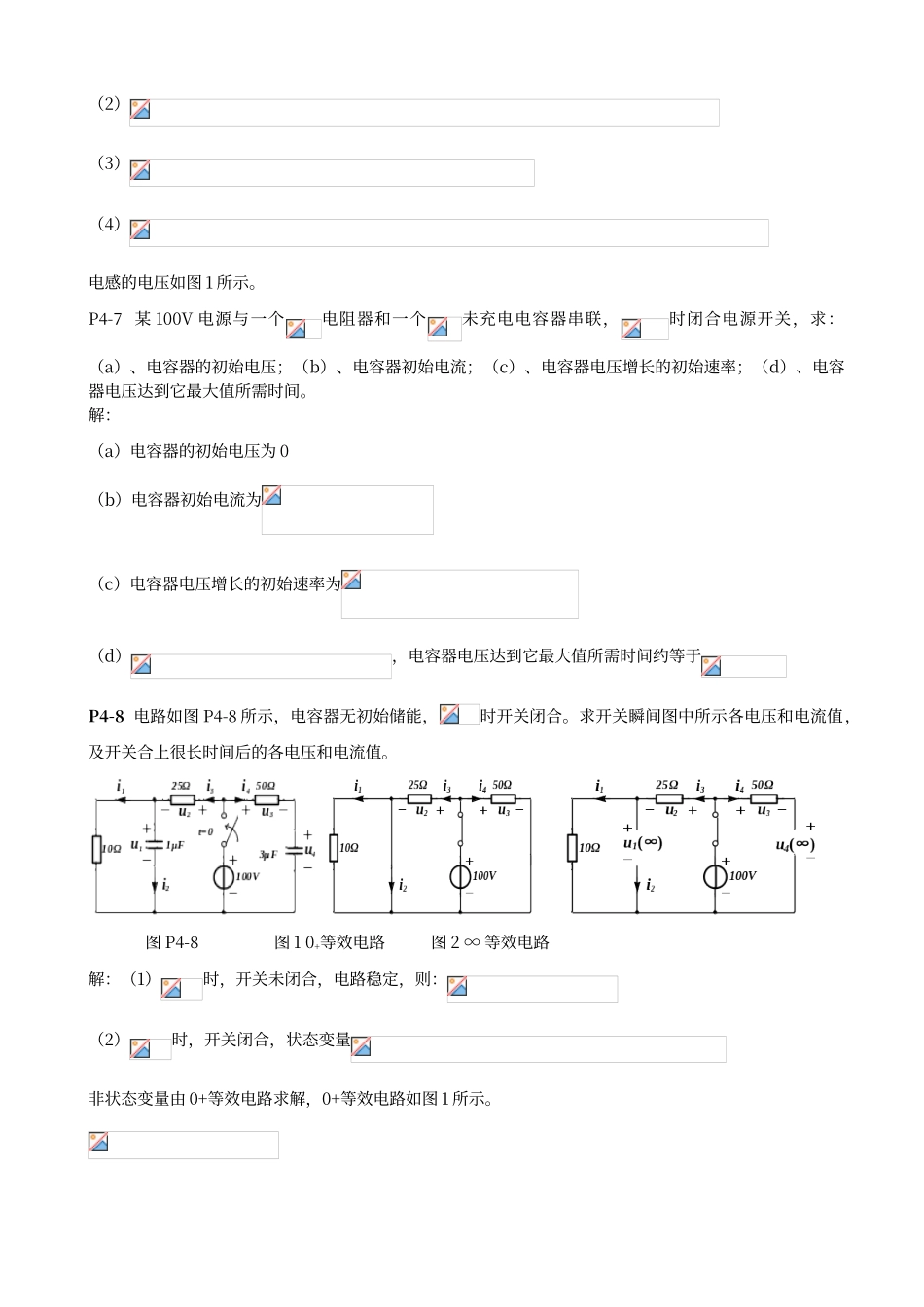
第 4 章 一阶电路的时域分析基础与提高题P4-1 电容器的端电压是时,存储电荷是多少?解:P4-2 充电到的电容器,通过一个电阻器放电,需要多长时间?何时的放电电流最大?最大值多少?解:,放电完毕约等于刚开始放电时电流最大,最大电流为P4-3 当电容器电压如图 P4-3 所示时,画出流过此电容器的电流波形图。假设电压与电流为关联参考方向。 图 P4-3 图 1解:关联参考方向,则电容电流,分段求解如下: (1)(2)(3)(4)(5)(6) 电容的电流如图 1 所示。P4-4 0.32tA 电流流过 150mH 电感器,求时,电感器存储的能量。解:电感器存储的能量当时,电感器存储的能量为 0.123WP4-5 由 20V 电源与电阻、电感组成的串联电路,合上开关后经过多长时间电流达到其最大值,最大值多少?设合上开关前电感无初始储能。解:,合上开关后经过约电流达到最大,最大电流为P4-6 当如图 P4-6 所示电流流过电感线圈时,求从到期间此线圈上产生的电压。 图 P4-6解:设电感电压与电流关联参考方向,则电感电压,分段求解如下:(1)(2)(3)(4)电感的电压如图 1 所示。P4-7 某 100V 电源与一个电阻器和一个未充电电容器串联,时闭合电源开关,求:(a)、电容器的初始电压;(b)、电容器初始电流;(c)、电容器电压增长的初始速率;(d)、电容器电压达到它最大值所需时间。解:(a)电容器的初始电压为 0(b)电容器初始电流为(c)电容器电压增长的初始速率为(d),电容器电压达到它最大值所需时间约等于P4-8 电路如图 P4-8 所示,电容器无初始储能,时开关闭合。求开关瞬间图中所示各电压和电流值,及开关合上很长时间后的各电压和电流值。图 P4-8 图 1 0+等效电路 图 2 ∞ 等效电路解:(1)时,开关未闭合,电路稳定,则:(2)时,开关闭合,状态变量非状态变量由 0+等效电路求解,0+等效电路如图 1 所示。 , ,(3)开关闭合很长时间电路处于稳态,∞等效电路如图 2 所示。 , , ,P4-9 图 P4-9 所示电路,当时,开关由位置 1 拨到位置 2。求开关拨到位置 2 瞬间及经很长时间后图中所标示的电流值。12t=0+-100VS140V+-12Ω20Ω18Ωi2i1120mH10Ω 图 P4-9 图 1 图 2解:(1)时,开关在位置 1,电感支路电流(2)时,开关在位置 2,状态变量非状态变量由 0+等效电路求解,0+等效电路如图 1 所示。由 KVL 得:,计算得:(3)开关闭合很长时间电路处于稳态,∞...