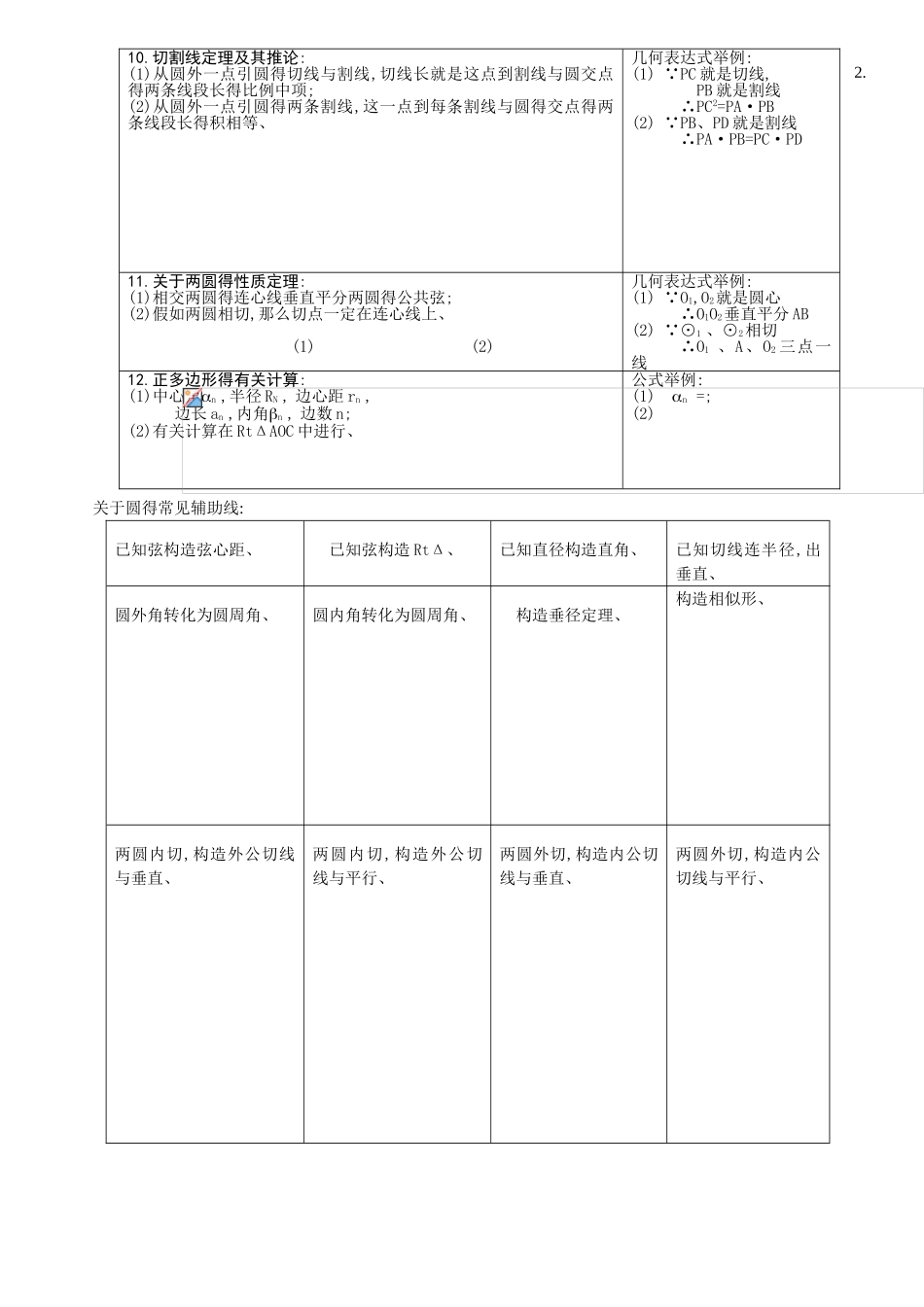
1、垂径定理及推论: 如图:有五个元素,“知二可推三”;需记忆其中四个定理,即“垂径定理”“中径定理” “弧径定理”“中垂定理”、 几何表达式举例: CD 过圆心 CD⊥AB2、平行线夹弧定理:圆得两条平行弦所夹得弧相等、几何表达式举例:3、“角、弦、弧、距”定理:(同圆或等圆中)“等角对等弦”; “等弦对等角”; “等角对等弧”; “等弧对等角”;“等弧对等弦”;“等弦对等(优,劣)弧”;“等弦对等弦心距”;“等弦心距对等弦”、几何表达式举例:(1) ∠AOB=∠COD∴ AB = CD (2) AB = CD∴∠AOB=∠COD4.圆周角定理及推论:(1)圆周角得度数等于它所对得弧得度数得一半;(2)一条弧所对得圆周角等于它所对得圆心角得一半;(如图)(3)“等弧对等角”“等角对等弧”;(4)“直径对直角”“直角对直径”;(如图)(5)如三角形一边上得中线等于这边得一半,那么这个三角形就是直角三角形、(如图)(1) (2)(3) (4)几何表达式举例:(1) ∠ACB=∠AOB∴ ……………(2) AB 就是直径∴ ∠ACB=90°(3) ∠ACB=90°∴ AB 就是直径(4) CD=AD=BD∴ ΔABC 就是 RtΔ 5.圆内接四边形性质定理:圆内接四边形得对角互补,并且任何一个外角都等于它得内对角、几何表达式举例: ABCD 就是圆内接四边形∴ ∠CDE =∠ABC∠C+∠A =180°6.切线得判定与性质定理:如图:有三个元素,“知二可推一”;需记忆其中四个定理、(1)经过半径得外端并且垂直于这条半径得直线就是圆得切线;(2)圆得切线垂直于经过切点得半径;※(3)经过圆心且垂直于切线得直线必经过切点;※(4)经过切点且垂直于切线得直线必经过圆心、几何表达式举例:(1) OC 就是半径 OC⊥AB∴AB 就是切线(2) OC 就是半径 AB 就是切线∴OC⊥AB(3) ……………7.切线长定理:从圆外一点引圆得两条切线,它们得切线长相等;圆心与这一点得连线平分两条切线得夹角、几何表达式举例: PA、PB 就是切线∴ PA=PB PO 过圆心∴∠APO =∠BPO8.弦切角定理及其推论:(1)弦切角等于它所夹得弧对得圆周角;(2)假如两个弦切角所夹得弧相等,那么这两个弦切角也相等;(3)弦切角得度数等于它所夹得弧得度数得一半、(如图) 几何表达式举例:(1) BD 就是切线,BC 就是弦∴∠CBD =∠CAB(2) ED,BC 就是切线∴ ∠CBA =∠DEF9.相交弦定理及其推论:(1)圆内得两条相交弦,被交点分成得两条线段长得乘积相等;(2)假如弦与直径垂直相交,那么弦得一半就是它分直径所成得两条线段长得比例中项、 ...