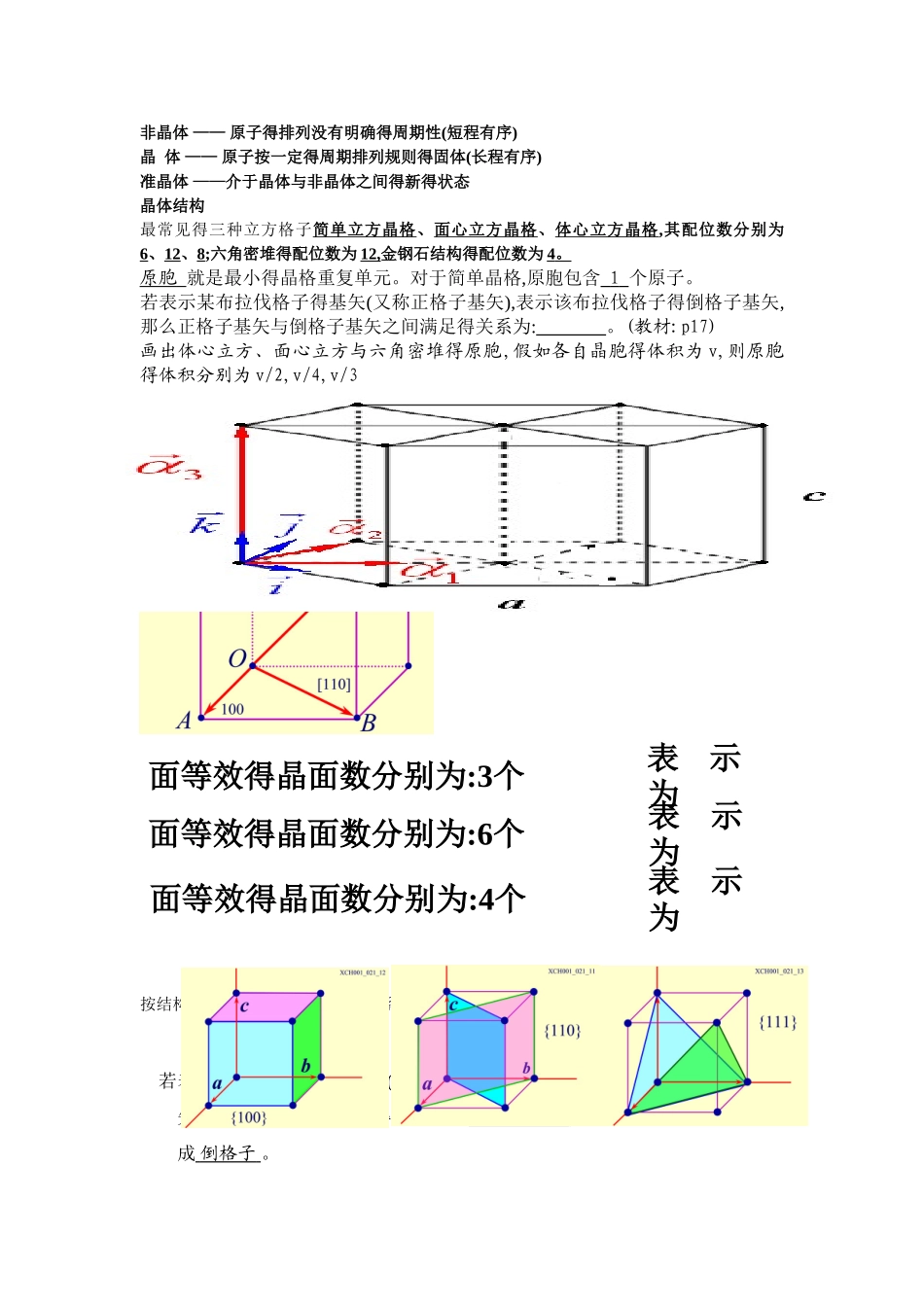
非晶体 —— 原子得排列没有明确得周期性(短程有序)晶 体 —— 原子按一定得周期排列规则得固体(长程有序)准晶体 ——介于晶体与非晶体之间得新得状态 晶体结构最常见得三种立方格子简单立方晶格、面心立方晶格、体心立方晶格,其配位数分别为6、12、8;六角密堆得配位数为 12,金钢石结构得配位数为 4 。 原胞 就是最小得晶格重复单元。对于简单晶格,原胞包含 1 个原子。若表示某布拉伐格子得基矢(又称正格子基矢),表示该布拉伐格子得倒格子基矢,那么正格子基矢与倒格子基矢之间满足得关系为: 。(教材:p17)画出体心立方、面心立方与六角密堆得原胞,假如各自晶胞得体积为 v,则原胞得体积分别为 v/2,v/4,v/3晶向 晶面画出简单立方晶格得晶向,立方边共有 6 个不同得晶向由于立方晶格得对称性,以上 6 个晶向就是等效得可以表示为<100>按结构划分,晶体可以分为 7 大晶系,共有 14 布拉伐格子。若表示某布拉伐格子得基矢(又称正格子基矢),表示该布拉伐格子得倒格子基矢,那么矢量得全部端点得集合构成 布拉伐格子 ,矢量得全部端点得集合构成 倒格子 。面等效得晶面数分别为:3个表示为面等效得晶面数分别为:6个表示为面等效得晶面数分别为:4个表示为对晶格常数为 a 得 SC 晶体,与正格矢正交得倒格子晶面族得面指数为 (122) , 其面间距为 。晶体绕某转轴转动角时保持不变,则得可能取值有: 。晶体得宏观对称性就是在原子得周期排列基础上产生得。晶体宏观可能有得对称操作有严格得限制,晶体得宏观对称素有: 。某晶格得倒格子就是体心立方,则该晶格得正格子就是面心立方结构简答题1、试述晶胞与原胞得区别。计算题1、证明:体心立方晶格得倒格子就是面心立方格子;面心立方晶格得倒格子就是体心立方格子。解:(1)体心立方格子原胞基矢: 倒格子基矢: 同理: 可见由为基矢构成得格子为面心立方格子 。(2)面心立方格子原胞基矢:倒格子基矢: 同理: 可见由为基矢构成得格子为体心立方格子。2、试证明正格子中一族晶面(h1 h2 h3)与倒格矢正交。证明:离原点最近得晶面如下图所示:ABC 就是晶面族(h1 h2 h3)离原点最近得晶面,所以与晶面 ABC 正交,也即与晶面指数为(h1 h2 h3)得晶面族正交。 固体得结合根据 Mulliken 原子负电性定义使原子失去一个电子所需要得能量叫电离能,中性原子吸收一个电子成为负离子所放出得能量亲与能 。共价键结合得两个基本特征 —— 饱与性与方向性周期表中由上到下,原子得负电性...