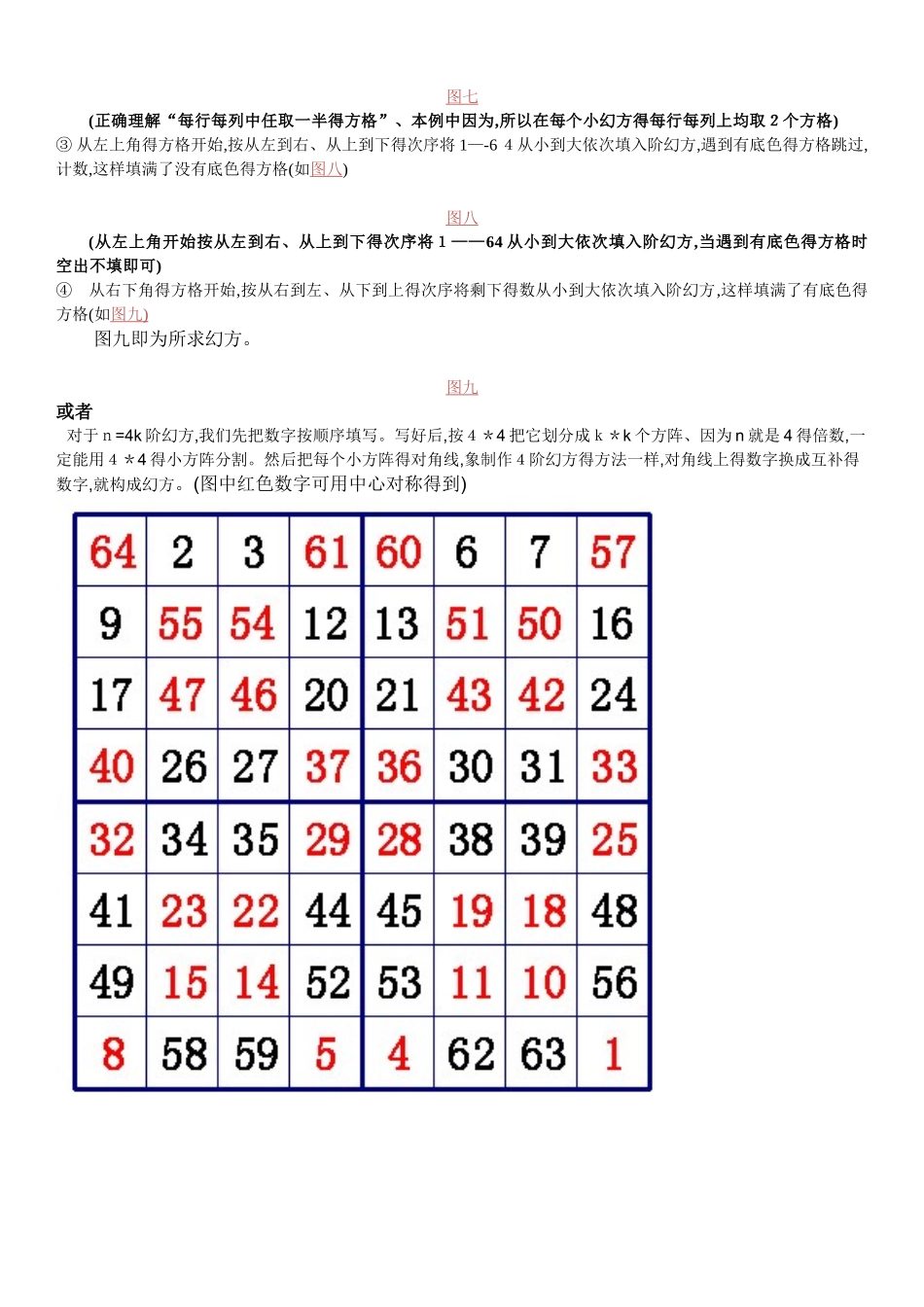
在一个由若干个排列整齐得数组成得正方形中,图中任意一横行、一纵行及对角线得几个数之与都相等,具有这种性质得图表,称为“幻方”。我国古代称为“河图”、“洛书”,又叫“纵横图”。1、奇数阶幻方—-罗伯特法(也有人称之为楼梯法)(如图一:以五阶幻方为例)奇数阶幻方 n 为奇数 (n=3,5,7,9,11……) (n=2×k+1,k=1,2,3,4,5……) 奇数阶幻方最经典得填法就是罗伯特法(也有人称之为楼梯法)。填写方法就是这样: 把 1(或最小得数)放在第一行正中; 按以下规律排列剩下得 n×n-1 个数: (1)每一个数放在前一个数得右上一格; (2)假如这个数所要放得格已经超出了顶行那么就把它放在底行,仍然要放在右一列; (3)假如这个数所要放得格已经超出了最右列那么就把它放在最左列,仍然要放在上一行; (4)假如这个数所要放得格已经超出了顶行且超出了最右列,那么就把它放在前一个数得下一行同一列得格内; (5)假如这个数所要放得格已经有数填入,处理方法同(4)。 这种写法总就是先向“右上”得方向,象就是在爬楼梯。口诀:1 居首行正中央,依次右上莫相忘上出格时往下放,右出格时往左放。 排重便往自下放,右上出格一个样 图一 2、单偶数阶幻方-—分区调换法(如图二:以六阶幻方为例)① 把阶得幻方均分成4个同样得小幻方 A、B、C、D(如图二 )图二 (注意 A、B、C、D 得相对位置不能改变,因为为奇数,所以 A、B、C、D 均为奇数阶幻方)② 用连续摆数法在 A 中填入构成幻方,同理,在 B 中填入、在 C 中填入、在D中填入均构成幻方()(如图三 )图三 (因为为奇数,所以 A、B、C、D 均为奇数阶幻方,必定可以用连续摆数法构造幻方)③ 在 A 得中间一行上从左侧得第二列起取个方格,在其它行上则从左侧第一列起取个方格,把这些方格中得数与 D中相应方格中得数字对调(如图四 ):图四 不管就是几阶幻方,在 A 中取数时都要从中间一行得左侧第二列开始;因为当时,,所以本例中只取了一个数)④ 在A中从最右一列起在各行中取个方格,把这些方格中得数与D中相应方格中得数字对调、(如图五)图五 3、双偶数阶幻方——轴对称法(如图三:以八阶幻方为例)① 把阶得幻方均分成 4 个同样得小幻方(如图六 )图六 ② 在左上角得小幻方每行每列中任取一半得方格加上底色 (以便于区分),然后以轴对称得形式在其它三个小幻方中标出方格(如图七 )图七 (正确理解“每行每列中任取一半得方格”、本例中因为,所以在每个小幻方得每行每列上均取2个方...