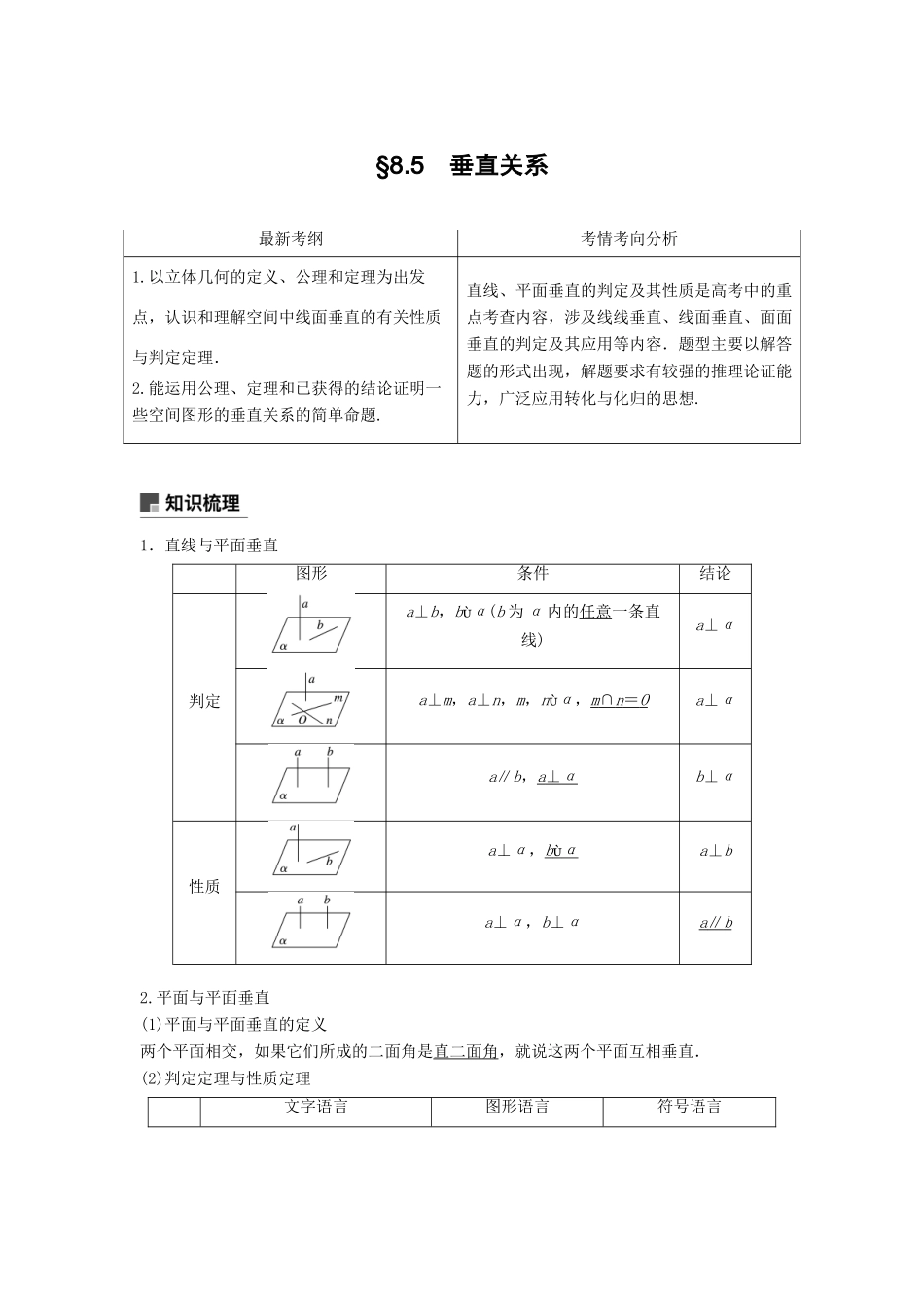
§8.5 垂直关系最新考纲考情考向分析1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面垂直的有关性质与判定定理.2.能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题.直线、平面垂直的判定及其性质是高考中的重点考查内容,涉及线线垂直、线面垂直、面面垂直的判定及其应用等内容.题型主要以解答题的形式出现,解题要求有较强的推理论证能力,广泛应用转化与化归的思想.1.直线与平面垂直图形条件结论判定a⊥b,bα(b 为 α 内的任意一条直线)a⊥αa⊥m,a⊥n,m,nα,m ∩ n = O a⊥αa∥b,a ⊥ α b⊥α性质a⊥α,b α a⊥ba⊥α,b⊥αa ∥ b 2.平面与平面垂直(1)平面与平面垂直的定义两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.(2)判定定理与性质定理文字语言图形语言符号语言判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直⇒α⊥β性质定理如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面⇒l ⊥ α 知识拓展重要结论(1)若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.(2)若一条直线垂直于一个平面,则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法).(3)垂直于同一条直线的两个平面平行.(4)一条直线垂直于两平行平面中的一个,则这条直线与另一个平面也垂直.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)直线 l 与平面 α 内的无数条直线都垂直,则 l⊥α.( × )(2)垂直于同一个平面的两平面平行.( × )(3)直线 a⊥α,b⊥α,则 a∥b.( √ )(4)若 α⊥β,a⊥β,则 a∥α.( × )(5)若直线 a⊥平面 α,直线 b∥α,则直线 a 与 b 垂直.( √ )(6)若平面 α 内的一条直线垂直于平面 β 内的无数条直线,则 α⊥β.( × )题组二 教材改编2.下列命题中错误的是( )A.如果平面 α⊥平面 β,那么平面 α 内一定存在直线平行于平面 βB.如果平面 α 不垂直于平面 β,那么平面 α 内一定不存在直线垂直于平面 βC.如果平面 α⊥平面 γ,平面 β⊥平面 γ,α∩β=l,那么 l⊥平面 γD.如果平面 α⊥平面 β,那么平面 α 内所有直线都垂直于平面 β答案 D解析 对于 D,若平面 α⊥平面 β,则平面 α 内的直线可能不垂直于平面 β,即与平面...