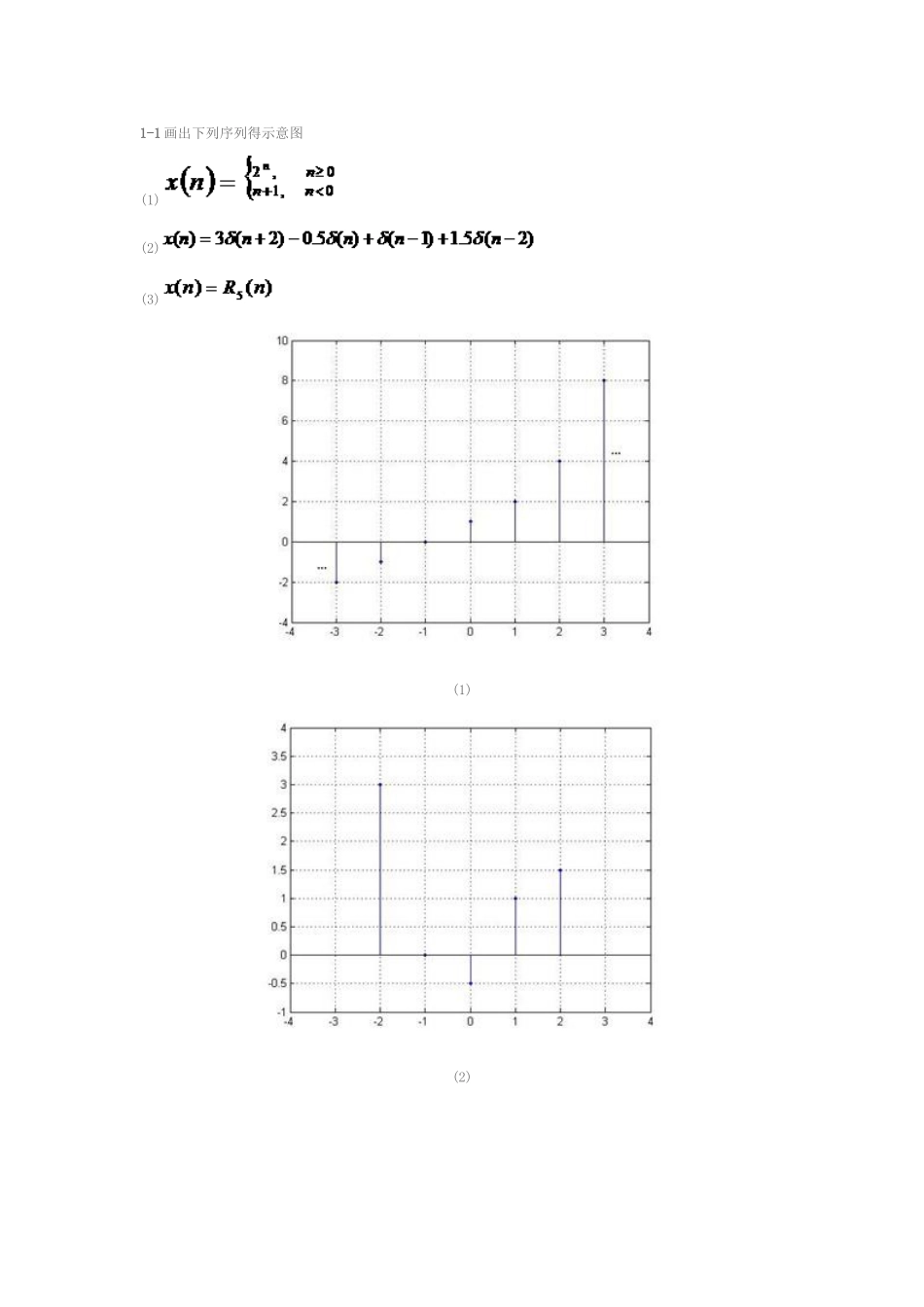
1-1 画出下列序列得示意图(1) (2) (3)(1)(2)(3)1-2 已知序列 x(n)得图形如图 1、41,试画出下列序列得示意图。图 1、41 信号 x(n)得波形(1) (2)(3) (4)(5) (6)(修正:n=4 处得值为 0,不就是 3) (修正:应该再向右移 4 个采样点)1-3 推断下列序列就是否满足周期性,若满足求其基本周期(1) 解:非周期序列;(2) 解:为周期序列,基本周期 N=5;(3) 解:,,取 为周期序列,基本周期。(4) 解: 其中,为常数,取, ,取则为周期序列,基本周期 N=40。1-4 推断下列系统就是否为线性得?就是否为移不变得?(1) 非线性移不变系统(2) 非线性移变系统 (修正:线性移变系统)(3) 非线性移不变系统(4) 线性移不变系统(5) 线性移不变系统 (修正:线性移变系统)1-5 推断下列系统就是否为因果得?就是否为稳定得?(1) ,其中 因果非稳定系统(2) 非因果稳定系统(3) 非因果稳定系统(4) 非因果非稳定系统(5) 因果稳定系统1-6 已知线性移不变系统得输入为 x(n),系统得单位脉冲响应为 h(n),试求系统得输出 y(n)及其示意图(1) (2) (3) 解:(1)(2)(3) 1-7 若采样信号 m(t)得采样频率 fs=1500Hz,下列信号经 m(t)采样后哪些信号不失真?(1) (2) (3) 解:(1) 采样不失真(2) 采样不失真(3), 采样失真1-8 已知,采样信号得采样周期为。(1) 得截止模拟角频率就是多少?(2)将进行 A/D 采样后,得数字角频率与得模拟角频率得关系如何?(3)若,求得数字截止角频率。解:(1) (2) (3) 1-9 计算下列序列得 Z 变换,并标明收敛域。(1) (2) (3) (4) (5) 解:(1) (2) (3) (4) ,,收敛域不存在(5) 1-10 利用 Z 变换性质求下列序列得 Z 变换。(1) (2) (3) (4) 解:(1) , (2) , (3) , (4) , 1-11 利用 Z 变换性质求下列序列得卷积与。(1) (2) (3) (4) (5) (6) 解:(1) , ,, , (2) , , , (3) , ,,(4) , , (5) ,, , (6) , ,, 1-12 利用得自相关序列定义为,试用得 Z 变换来表示得 Z 变换。解: 1-13 求序列得单边 Z 变换 X(Z)、解: 所以:1-14 试求下列函数得逆 Z 变换(1) (2) (3) (4) ,整个 Z 平面(除 z=0 点)(5) (6) 解:(1) (2) , (3) (4) (5) (6) 1-15 已知因果序列得 Z 变换如下,试求该序列得初值及终值。(1)(2)(3)解:(1) ,(2) ,(3) ,1-16 若存在一离散时间系统得系统函数,根据下面得收敛域,求系统得单位脉冲响应,并推断系统就是否因果?就是否稳定?...